Курсовая работа: Беселеві функції

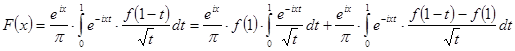.(26)

Розглянемо інтеграл, що фігурує в правої частини формули (20). Заміняючи на , знайдемо:

,

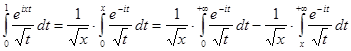але, замінивши на , одержимо:

.

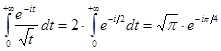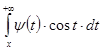Якщо позитивно, убуває й прагнути до нуля при , то й 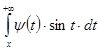, а отже, і 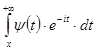є при , тому

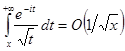при ,

звідки

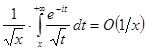при .

Отже, одержуємо асимптотичне подання:

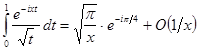при . (27)

Розглянемо тепер інтеграл, що фігурує в другому складати^ся правої частини формули (20). Маємо:

,

.

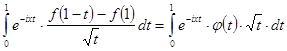Очевидно, двічі безупинно на , але існують і , тому стає безупинно диференцуєма на . Інтегрування вроздріб дає:

,

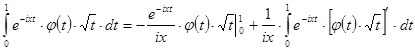де перший доданок правої частини є при , а інтеграл у другому мажорирується інтегралом, що складається при нижній межі

,

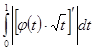який сходиться, тому що

при ;

отже, другий доданок є теж при .

Отже, маємо:

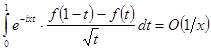при . (28)

З (26), (27), (28) одержуємо шукане асимптотичне подання:

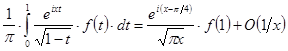при . (29)

Із цієї формули, переходячи до сполучених величин, знайдемо ще:

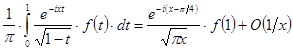при . (29')

Формули (29) і (29`) вірні й для функцій .

Висновок асимптотичної формули для Jn(x)