Курсовая работа: Беселеві функції

Цим доведено, що при система функцій

на інтервалі є ортогональної щодо ваги .

Переходячи до межі при в співвідношенні

і використовуючи правило Лопиталя, одержимо при всякому

, (24)

отже, якщо є нулем функції , те

. (24`)

Таким чином, при кожному всякій безперервній функції на , що задовольняє вимозі

,

поставлений у відповідність ряд Фур'є-Беселя

, (25)

коефіцієнти якого визначаються формулами

. (25`)

Можна довести, що система функцій на , ортогональна щодо ваги , замкнута. Зокрема, якщо ряд Фур'є-Беселя (25) рівномірно сходиться до його безперервної функції, що породжує.

Можна показати, що якщо й безперервна на й функція, то ряд Фур'є-Беселя цієї функції сходиться до неї при .

6. Асимптотичне подання Беселевих функцій із цілим індексом для більших значень аргументу

Нехай – позитивна функція й – яка-небудь функція для досить більших значень . Запис

при

означає, що найдуться такі числа й M, що при маємо .

Подібний запис уживається й в інших аналогічних випадках. Наприклад, якщо – позитивна функція й – яка-небудь функція, визначені для досить малих позитивних значень , то запис

при

означає, що найдуться такі числа й , що на .

Допоміжна лема

Якщо двічі безупинно диференцюєма на , то для функції

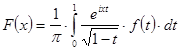
має місце асимптотичне подання

при .