Курсовая работа: Чисельні методи розвязування крайових задач для звичайних диференціальних рівнянь

За формулою Рунге

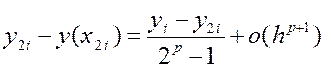
Таким чином, із точністю до (величина більш високого порядку малості) при h→0 похибка методу має вигляд:

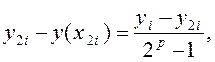
де y_i – наближене значення, отримане в точці з кроком h ; y_2i – із кроком h/2 ; p - порядок методу; y(x_2i ) - точний розв’язок задачі.

Формула Рунге:

.

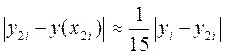Збіжність різницевої схеми

Постановка задачі

Універсальним методом наближеного розв’язання, є метод скінченних різниць. Як задачі представлені у вигляді систем нелінійних рівнянь у часткових, які розглядаються у області

Розв’язок задачі в має додаткові умови:

1) умови при називають початковими умовами;

2) умови на границі області — крайовими або граничними умовами.

Задача з початковими умовами – називається задачею Коші.

Нехай . Тоді для функції маємо задачу:

(1)

(2)

де и - диференціальні оператори задачі і крайових умов. Припустимо ,що відповідно задачі (1-2) поставлені коректно, тобто оператори А и R; область D и її границі Г такі, що при виборі відповідних класів функцій і правих частин у рівняннях (1) и (2) розв’язок існує, і залежить від початкових даних.

Різницева схема

Введемо у області сітку , яка складається з множини внутрішніх вузлів і множини граничних вузлів :

Далі розглянемо сіткові функції і з їх допомогою побудуємо наближений розв’язок задачі (1-2). Для цього відносно сформулюємо "різницеву задачу", заміняючи оператори задачі і і їх сітковим аналогами и. Тоді на сітковому шаблоні маємо

(3)

(4)

Задачу (3)-(4) назвемо різницевою схемою для задачі (1)-(2). Звичайно це алгебраїчна система рівнянь відносно .

При переході від початкової задачі (1)-(2) до її різницевого аналогу (3)-(4) особливо важливі 3 групи питань:

- існування, єдиність і алгоритм побудови різницевого розв’язку ;

- при яких умовах різницевий розв’язок збігається до точного розв’язку і яка при цьому швидкість збіжності;

- як конкретно вибирати сітку і побуду