Курсовая работа: Чисельні методи розвязування крайових задач для звичайних диференціальних рівнянь

Знайдемо вирази для коефіцієнтів системи рівнянь з невідомими . Підставляючи в останній вираз , отримаємо

Перший з інтегралів у цьому виразі обчислимо по частинах:

Оскільки за граничних умов (11.60) використовуються , базисних функцій від до і всі вони в точках і дорівнюють 0, то

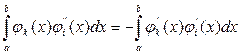
Тоді вираз для обчислення набуває вигляду:

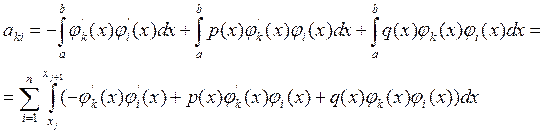(11.64)

Для обчислення треба знайти значення похідних від фінітних функцій. Із цією метою диференціюємо (11.61) і отримуємо:

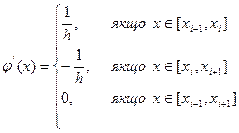(11.65)

Функція відмінна від нуля тільки на інтервалі . Крім того, на одному і тому ж інтервалі ненульовими є дві базисні функції і їх похідні з сусідніми індексами (рис. 3), тобто на інтервалі відмінні від нуля , , , і т. д.

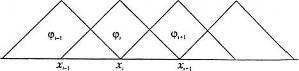
рис. 3. Система фінітних функцій.

У виразі для (11.64) добутки , , можна вважати відмінними від нуля тому, що на елементарному інтервалі не дорівнюють нулю фінітні функції та їх похідні, які мають сусідні індекси у випадках, коли . А це означає, що

для , (11.66)

тобто матриця системи (11.62) є тридіагональною матрицею. її ненульові елементи обчислюються таким чином. Формули для діагональних елементів отримаємо, приймаючи у виразі (11.64):

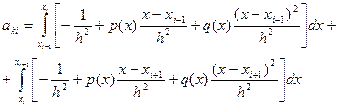(11.67)

Для , отримаємо формули для елементів правої бічної діагоналі матриці :

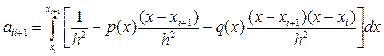, (11.68)

а для - лівої;

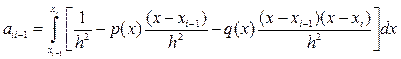
Три останні вирази визначають систему алгебраїчних рівнянь (11.62) для невідомих коефіцієнтів .

Розглянемо розв’язання задачі (11.59) у випадку неоднорідних граничних умов

, (11.70)

і зведемо її до розв'язання задачі з однорідними граничними умовами. Для цього введемо заміну:

, де .

Двічі диференціюючи цю функцію і підставляючи вирази для похідних у рівняння (11.59), отримаємо крайову задачу з однорідними граничними умовами:

,

, . (11.71)