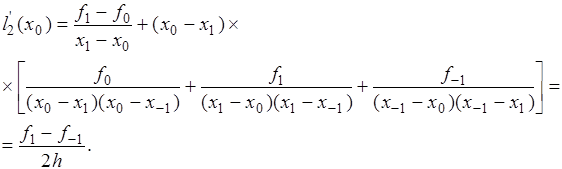Курсовая работа: Численные методы

.

Если процесс приведения матрицы А к форме Р был регулярным, то

 ñîîòâåòñòâèè ñ òåîðåìîé ñîáñòâåííûì âåêòîðîì ìàòðèöû А для собственного значения будет вектор

Таким образом, задача вычисления собственных векторов матрицы А решена.

ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ .

Пусть имеется функция которую необходимо продифференцировать несколько раз и найти эту производную в некоторой точке.

Если задан явный вид функции, то выражение для производной часто оказывается достаточно сложным и желательно его заменить более простым. Если же функция задана только в некоторых точках (таблично), то получить явный вид ее производных ввобще невозможно. В этих ситуациях возникает необходимость приближенного (численного) дифференцирования.

Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом (Лагранжа, Ньютона) и производная функции приближенного заменяется соответствующей производной интерполяционного многочлена

Рассмотрим простейшие формулы численного дифференцирования, которые получаются указанным способом.

Будем предполагать, что функция задана в равностоящих узлах

Ее значения и значения производных в узлах будем обозначать

Пусть функция задана в двух точках и ее значения

Посстроим интерполяционный многочлен первой степени

Производная равна

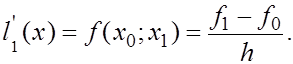
Производную функцию в точке приближенно заменяем производной интерполяционного многочлена

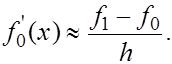(1)

Величина называется первой разностной производной .

Пусть задана в трех точках

Интерполяционный многочлен Ньютона второй степени имеет вид

Берем производную

В точке она равна