Курсовая работа: Численные методы

Кроме того, доказанные неравенства , обеспечивают устойчивость счета по рекуррентным формулам (6). Последнее означает, что погрешность,внесенная на каком-либо шаге вычислений, не будет возрастать при переходе к следующим шагам.

Действительно, пусть в формуле (6) при вместо вычислена величина

Тогда на следующем шаге вычислений, т.е. при

вместо

получим величину и погрешность окажется равной

Отсюда получаем, что ,т.е. погрешность не возрастает.

Подсчитаем число арифметических действий, выполняемых при решении задачи (1), (2) методом прогонки.

По формулам (4), что реализуемые с помощью шести арифметических действий, вычисления производятся раз, по формуле (6) выполняется 5 арифметических действий, наконец по формуле (3), требующей всего два действия, вычисления осуществляются раз. Итак в методе прогонки всего затрачивается

арифметических действий, т.е. число действий растет линейно относительно числа неизвестных

При решении же произвольной системы линейных алгебраических уравнений методом Гаусcа число действий пропорционально кубу числа неизвестных.

ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ.

Большое число задач математики и физики требует отыскания собственных значений и собственных векторов матриц, т.е. отыскания таких значений +, для которых существуют нетривиальные решения однородной системы линейных алгебраических уравнений

, (1)

и отыскания этих нетривиальных решений.

Здесь -квадратная матрица порядка m , - неизвестный вектор - столбец.

Из курса алгебры известно, что нетривиальное решение системы (1) существует тогда и только тогда, когда

, (2)

где Е - единичная матрица. Если раскрыть определитель , ïîëó÷àåòñÿ алгебраическое уравнение степени m относительно.Таким образом задача отыскания собственных значений сводится к проблеме раскрытия определителя по степеням и последующему решению алгебраического уравнения m - й степени.

Определитель называется характеристическим (или вековым ) определителем , а уравнение (2) называется характеристическим (или вековым ) уравнением .

Различают полную проблему собственных значений , когда необходимо отыскать все собственные значения матрицы А и соответствующие собственные векторы, и частичную проблему собственных значений , когда необходимо отыскать только некоторые собственные значения, например, максимальное по модулю собственное значение .

Метод Данилевского развертывание векового определителя.

Определение. Квадратная матрица Р порядка m называетсяподобной матрице А , если она представлена в виде

,

где S - невыродженная квадратная матрица порядка m .

ТЕОРЕМА . Характеристический определитель исходной и подобной матрицы совпадают .

Доказательство .

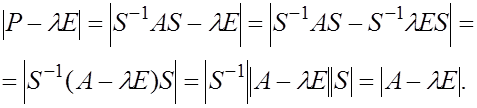
Идея метода Данилевского состоит в том, что матрица А подобным преобразованиям приводится, к так называемой нормальной форме Фробениуса