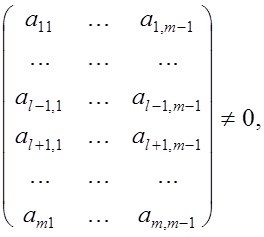Курсовая работа: Численные методы
PAx=Pf, (21)
где Р - некоторая матрица перестановок.
Теоретическое обоснование метода Гаусса с выбором главного элемента содержится в следующей теореме.
ТЕОРЕМА 1. Если ![]() то существует матрица перестано-
то существует матрица перестано-
вок Р такая, что матрица РА имеет отличные от нуля угловые ми-
норы.
Доказательство в п.4.
СЛЕДСТВИЕ. Если ![]() то существует матрица престана-
то существует матрица престана-
вок Р такая, что справедливо разложение
РА=LU, (22)
где L - нижняя треугольная матрица с отличными от нуля диагональными элементами и U- верхняя треугольная матрица с единичной главной диагональю. В этом случае для решения системы (1) можно применять метод Гаусса с выбором главного элемента.
4. Доказательство теоремы 1. Докажем теорему индукцией по числу m -порядку матрицы А .
Пусть m=2 , т.е.
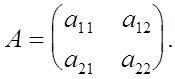
Если ![]() то утверждение теоремы выполняется при Р=Е , где Е - единичная матрица второго порядка. Если
то утверждение теоремы выполняется при Р=Е , где Е - единичная матрица второго порядка. Если ![]() , то
, то ![]() , т.к.
, т.к. ![]() При этом у матрицы
При этом у матрицы
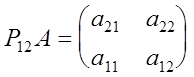
все угловые миноры отличны от нуля.
Пусть утверждение теоремы верно для любых квадратных матриц порядка m -1 . Покажем, что оно верно и .для матриц порядка m. Ра зобьем матрицу А порядка m на блоки
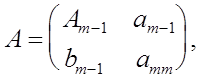
где
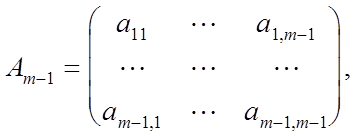
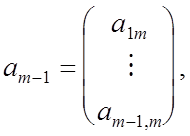
![]()
Достаточно рассмотреть два случая :![]() и
и ![]() . В первом случае по предположению индукции существует матрица перестановок
. В первом случае по предположению индукции существует матрица перестановок ![]() порядка m-1 такая, что
порядка m-1 такая, что ![]() имеет отличные от нуля угловые миноры. Тогда для матрицы перестановок
имеет отличные от нуля угловые миноры. Тогда для матрицы перестановок
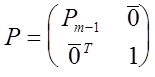
имеем
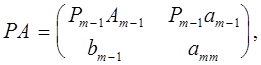
причем ![]() . Тем самым все угловые миноры матрицы РА отличны от нуля.
. Тем самым все угловые миноры матрицы РА отличны от нуля.
Рассмотрим второй случай, когда![]() . Т.к.
. Т.к.![]() , найдется хотя бы один отличный от нуля минор порядка m-1 матрицы А, полученный вычеркиванием последнего столбца и какой-либо строки. Пусть, например,
, найдется хотя бы один отличный от нуля минор порядка m-1 матрицы А, полученный вычеркиванием последнего столбца и какой-либо строки. Пусть, например,