Курсовая работа: Численные методы

Нахождение коэффициентов по формулам (4), (5) называется прямой прогонкой . После того, как прогоночные коэффициенты найдены, решение системи (1), (2) находится по рекуррентной формуле (3), начиная с Для начала счета по этой формуле требуется знать , которое определяется из уравнений

И равно

.

Нахождение по формулам

(6)

называется обратной прогонкой. Алгоритм решения системы (1), (2) определяемый формулами (4)-(6) называется методом прогонки .

Метод прогонки можно пременять, если знаменатели выражений (4), (6) не обрщаются в нуль.

Покажем, что для возможности применения метод прогонки достаточно потребовать, чтобы коэффициенты системы (1), (2) удовлетворяли условиям

(8)

Сначала докажем по индукции, что при условиях (7), (8) модули прогоночных коэффициентов не превосходят единицы. Согласно (5), (8) имеем . Предположим,что для некоторого и докажем, что

Прежде всего для любых двух комплексных чисел и докажем неравенство

Из неравенства треугольника имеем

Откуда

Вернемся теперь к доказательству , если . Согласно имеем оценку

а, используя (7) , получаем

т.е. знаменатели выражений (4) не обращаются в нуль.

Более того

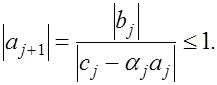
Следовательно,

Далее, учитывая второе из условий (8) и только что доказанное неравенство , имеем

т.е. не обращается в нуль и знаменатель в выражении для .

К аналогичному выводу можно прийти и в том случае, когда условия (7), (8) заменяются условиями