Курсовая работа: Дифференциальные уравнения

Запишем ОЛДУ и найдём корни его характеристического уравнения:

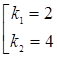
Общее решение имеет вид:

Найдём решение частное:

,

где С₁ и С₂ – решения системы дифференциальных уравнений

По теореме Крамера:

Интегрируя выражения, получим:

Следовательно, решение будет выглядеть так:

Найдём значения С₁ и С₂