Курсовая работа: Динамический расчет следящих систем

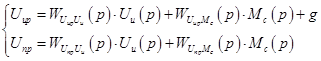(19)

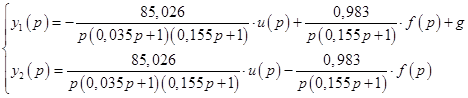(20)

Для вывода уравнений вход-выход оба уравнения (20) умножим на общий знаменатель и перейдем к оригиналам:

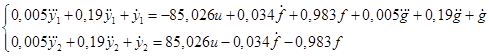(21)

6.АНАЛИЗ СВОЙСТВ ЗАДАННОЙ ЧАСТИ СЛЕДЯЩЕЙ СИСТЕМЫ.

6.1 Проверка управляемости.

Проверку проводим по уравнению (18) при с помощью критерия управляемости.

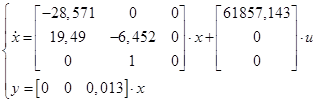
Обычно предполагают, что объект управления (система) обеспечивает возможность изменения его переменных состояния и регулируемых величин в соответствие с целью управления с помощью управлений, приложенных к нему. Однако ясно, что в общем случае не всякий объект управления допускает такую возможность, т.е. не каждый объект является управляемым. Следует отметить, что это свойство – управляемости – зависит исключительно от внутренних свойств объекта.

Для оценки управляемости систем используется критерий Калмана, в основе которого лежит матрица управляемости:

,

где - размерность вектора переменных состояния.

В нашем случае , значит:

, ,

,

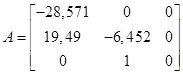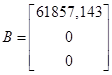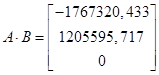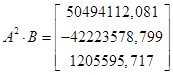
Матрица Uбудет иметь вид:

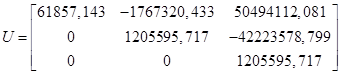
Так как и определитель матрицы Uне равен нулю, то объект является полностью управляемым.

6.2 Проверка наблюдаемости заданной части системы.

Для формирования модального управления необходимо измерить переменные состояния системы. Но часто бывает так, что переменные состояния недоступны для прямого измерения с помощью каких-либо датчиков. Обычно измеряются выходные величины объекта (системы), такие, как регулируемые переменные, ошибка системы, положение регулирующего органа, скорость изменения регулируемой величины. Отсюда возникает задача наблюдения, которая состоит в необходимости восстановления значений переменных состояния системы по результатам измерения (наблюдения) некоторых выходных величин системы, а это оказывается возможным только в том случае, если объект (система) является наблюдаемым.

Для определения наблюдаемости системы воспользуемся критерием наблюдаемости, предложенный Калманом. Этот критерий использует матрицу наблюдаемости, которая для систем имеет вид:

,

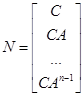где - размерность вектора переменных состояния.

В нашем случае , значит:

, ,

,

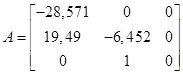Матрица Nбудет иметь вид: