Курсовая работа: Динамический расчет следящих систем

Так как и определитель матрицы Nне равен нулю, то объект является вполне наблюдаемым.

6.3 Проверка устойчивости нескорректированной системы.

Проверка устойчивости нескорректированной замкнутой системы обычно проводится для того, чтобы убедится, нельзя ли построить требуемую следящую систему лишь на основе заданных элементов. Если выходной сигнал измерителя рассогласования подать на вход усилителя, то получится замкнутая система, структурная схема которой приведена на рисунке 6.

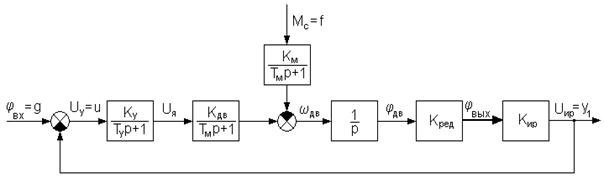
Рис.6.Структурная расчетная схема нескорректированной замкнутой системы.

Для использования алгебраического критерия Гурвица необходимо знать характеристический полином исследуемой замкнутой системы. Таким образом, получим:

Необходимым, но недостаточным условием устойчивости является положительность всех коэффициентов полинома, но поскольку старшая степень полинома равна трем, то для проверки устойчивости также необходимо воспользоваться частным случаем алгебраического критерия Гурвица – критерием Вышнеградского. Согласно последнему, система будет устойчивой, если будет выполнено условие:

,

где - коэффициенты характеристического полинома при переменной р в соответствующих степенях.

Подставим коэффициенты нашего характеристического полинома в последнее выражение и проверим выполнение этого условия:

как видно, условие не выполняется.

Следовательно, для заданной замкнутой системы условие не выполняется, то можно сделать вывод о том, что заданная часть системы является неустойчивой.

7. СИНТЕЗ УСТРОЙСТВА УПРАВЛЕНИЯ.

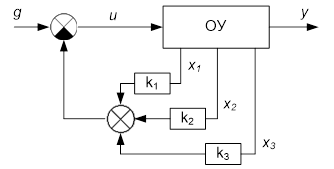
Рис.7. Структурная схема следящей системы.

Допустим, заданная часть системы описывается уравнением:

, (24)

где .

Уравнение устройства управления выберем:

(25)

Здесь , и - полиномы, которые нужно определить так, чтобы замкнутая система (24), (25) имела требуемые показатели качества:

Для вывода расчетных соотношений запишем уравнение замкнутой системы:

(26)

Чтобы упростить схему управляющего устройства, примем: