Курсовая работа: Элементы тензороного исчисления

то мы видим, что переход от первоначальных переменных к определяется формулой

где

Это преобразование, следовательно, также линейное.

Говорят, что совокупность преобразований образует группу, когда она удовлетворяет следующим условиям: 1) если преобразования от к и от кпринадлежат данной совокупности, то преобразование от к также принадлежат к ней; 2) совокупность преобразования содержит тождественное и обратное преобразования.

Таким образом, совокупность линейных преобразований образует группу.

§ 2. Индексные обозначения

Если нам дана совокупность трех независимых переменных, то они могут быть обозначены тремя различными буквами, например x , y , z , но мы считаем более удобным обозначать переменные данной совокупности одной и той же буквой, различая их посредством индексов. Таким образом, мы можем записать три переменные в виде, или в более компактной форме:

(2.1)

Здесь мы написали индекс внизу, но в равной мере мы могли бы использовать вместо этого верхний значок, так что переменные были бы записаны в виде или

(2.2)

Однородная линейная функция переменных обычно записывается в виде

(2.3)

где - константы. Таким образом, коэффициенты линейной формы могут быть записаны в виде

Объекты, которые, подобно и , зависят только от одного индекса, называются объектами первого порядка, а отдельные буквы с индексами и называются элементами или составляющими объекта. Объекты первого порядка, имеющие три составляющие, назовем трехмерными. Имеются два типа объектов первого порядка, а именно те, у которых индекс вверху, и те, у которых индекс внизу; следовательно, все объекты первого порядка принадлежат к одному из двух типов

(2.4)

С другой стороны, однородная квадратичная функция трех переменных имеет вид

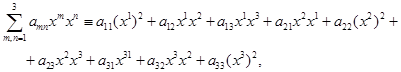(2.5)

где а_тп - константы. Мы видим, что коэффициенты квадратичной формы зависят от двух индексов и записываются так:

Составляющие этого объекта преобразуются следующим образом:

Следовательно, эта формула дает один из способов, с помощью которого может быть преобразован объект первого порядка. Любой объект, составляющие которого преобразуются по этому закону, называется контравариантным вектором. Таким образом, есть контравариантный вектор, если при линейном преобразовании переменных (1.1) его преобразованные составляющие определяются формулами

(2.6)

Имеется и другой способ преобразования элементов объекта первого порядка. Мы уже видели, что коэффициенты линейной формы переменных xтакже образуют объект первого порядка. Таким образом, коэффициенты линейной формы являются составляющими объекта. Предположим, что составляющие преобразуются таким образом, что линейная форма остается инвариантной относительно преобразования переменных (1.1). Если мы обозначим через новые составляющие объекта (после преобразования), то получим

,

так как эта линейная форма есть инвариант. Тогда из (1.3) следует