Курсовая работа: Элементы тензороного исчисления

Для произвольных тензоров полное умножение производится по правилу "многочлен на многочлен". Результатом полного умножения тензора ранга р на тензор ранга qявляется тензор ранга р -q .

Если X и Y - тензоры одинакового ранга, то полное умножение совпадает с введенным ранее скалярным произведением в пространстве .

§6. Поднятие и опускание индексов

Предположим, что X - это тензор типа (r,s) . Давайте выберем его α -тый нижний индекс: Символы, используемые для других индексов, несущественны. Поэтому, мы обозначили их точками. Затем рассмотрим тензорное произведение

(6.1)

Здесь g - дуальный метрический тензор с элементами. На следующем шаге свернем (6.1) по паре индексов k и q . Для этой цели мы заменяем их на s и проводим суммирование:

(6.2)

В целом вся операция (6.2) называется поднятием индекса. Эта операция обратима. Обратная операция называется опусканием индексов:

(6.3)

Подобно (6.2), операция опускания индекса (6.3) включает в себя две операции над тензорами: тензорное произведение и свертку.

§7.Тензоры в криволинейных координатах

Мы будем рассматривать область аффинного пространства, отнесенную к криволинейным координатам . Радиус-вектор х произвольной точки М области , отсчитываемый от фиксированной точки О, будет выражаться функцией

(7.1)

достаточное число раз непрерывно дифференцируемой. В дальнейшем мы предполагаем, что все рассматриваемые точки принадлежат области .

Для ориентации в строении данной координатной системы весьма полезны координатные линии. Так мы будем называть кривые, вдоль которых меняется лишь одна из координат а остальные остаются постоянными. Рассмотрим, например, координатную линию . Это значит, что закреплены на постоянных значениях, так что радиус-вектор х (7.1) остается функцией одного лишь ;мы получаем кривую, отнесенную к параметру .

Через каждую точку М пройдет одна и только одна координатная линия , именно, если закрепить на значениях, которые они имеют в точке М.Частная производная дает касательный вектор к координатной линии. Все сказанное справедливо и для любых координатных линий, так что через каждую точку М проходят п координатных линий с касательными векторами . Эти векторы мы будем обозначать кратко

(7.2)

Они, как мы знаем, всегда линейно независимы, ипотому в каждой точке М могут быть приняты за векторы аффинного репера Таким образом, задание криволинейных координат в области влечет появление в каждой ее точке М вполне определенного аффинного репера Этот аффинный репер мы будем называть локальным репером в точке М.

Когда в качестве частного случая криволинейных координат мы берем аффинные координаты, функция (7.1) принимает вид:

(7.3)

илокальный репер в каждой точке М имеет те же векторы, что и основной репер, на котором построена данная аффинная координатная система.

Для рассмотрения локальных реперов имеются глубокие основания. Именно вспомним те простые свойства, которыми обладали аффинные координаты точек: приращения этих координат при переходе из точки в точку выражали координаты вектора смещения :

поскольку

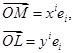
(говоря о координатах вектора, мы всегда будем иметь в виду его аффинные координаты; криволинейные координаты для векторов не имеют смысла). В этом, можно сказать, и состояла сущность аффинных координат точек.

Для криволинейных координат эти простые свойства теряются. Однако мы находим их снова, если рассматривать криволинейные координаты в бесконечно малой окрестности данной точки М.

Смещаясь из точки в бесконечно близкую точку,мы находим вектор смещения , как приращение радиуса вектора х точки М: