Курсовая работа: Элементы тензороного исчисления

(7.12)

Таким образом, переход от одних криволинейных координат к другим, влечет за собой преобразование координат тензорного поляпо закону (7.12). При этом частные производные по и обратно берутся в той же точке М, как и координаты тензора, что и отмечено в записи.

§8. Примеры вычислений

Пример 1 (Динамика частицы)

В качестве простого приложения тензорного исчисления чуть переформулируем уравнения классической динамики материальной точки.

Второй закон Ньютона в компонентах записывается как

(8.1)

Откуда сразу видна его ковариантность по отношению к преобразованиям из группы О (3). Если силовое поле потенциально, то

(8.2)

Умножая обе части (8.1) на и свертывая по индексам, получим

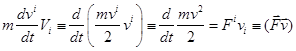
т.е.

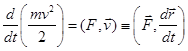(8.3)

Вводя кинетическую энергию частицу и элементарную работу силы , придем к теореме живых сил.

(8.4)

Инвариантной относительно ортогональных преобразований. Для потенциального стационарного поля сил