Курсовая работа: Элементы тензороного исчисления

(7.4)

Это значит, что вектор смещения в локальном репере имеет координа-ты, равные приблизительно приращениям .

Итак, для бесконечно малых смещений из точки М приращения криволинейных координат снова выражают координаты вектора смещения , если эти последние вычислять в локальном репере в точке М, пренебрегая бесконечно малыми высшего порядка.

Таким образом, при помощи локального репера криволинейным координатам возвращаются свойства аффинных координат, правда, теперь уже лишь в бесконечно малой окрестности данной точки.

Можно сказать также, что приращения криволинейных координат в бесконечно малой окрестности точки М совпадают с точностью 1-го порядка с аффинными координатами относительно локального репера, построенного в точке М.

Естественно, что, занимаясь геометрией аффинного пространства в криволинейных координатах, мы постоянно будем сталкиваться с локальными реперами.

Выясним теперь, что происходит с локальными реперами, когда криволинейные координаты подвергаются преобразованию

(7.5)

которое предполагается однозначно обратимым и непрерывно дифференцируемым в обе стороны. Выражая, обратно,

(7.6)

мы можем считать в уравнении (7.1) радиус-вектор х сложной функцией от . Частная производная по выразится тогда по известной формуле:

В правой части по i , конечно, происходит суммирование. Заметим, что мы будем без стеснения прилагать обычные формулы дифференцирования к выражениям, содержащим векторы, так как справедливость этих формул устанавливается тривиальным образом: достаточно свести дифференцирование векторов к дифференцированию их координат. Окончательно получаем:

(7.7)

Итак, преобразование криволинейных координат влечет за собой преобразование локального репера в каждой точке М, причем векторы нового локального репера разлагаются по векторам старого с коэффициентами 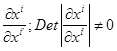.Сравнивая с нашей прежней записью преобразования аффинного репера

мы видим, что (7.7) представляет собой ее частный случай, когда

(7.8)

ароль векторов играют .

Рассмотрим теперь произвольное тензорное поле, например, . Точка М может при этом пробегать всю область или только некоторую поверхность в ней, или даже линию в зависимости от того, где тензорное поле задано.

Координаты тензора можно вычислять относительно любого аффинного репера. Однако в дальнейшем мы всегда будем считать, что аффинное пространство (по крайней мере в пределах области ) отнесено к каким-либо криволинейным координатам . Тогда в каждой точке М возникает локальный репер, и координаты тензора мы будем брать относительно именно этого репера. Эти координаты мы будем кратко называть координатами тензора в данной системе криволинейных координат .

Когда в дальнейшем мы будем говорить о тензорном поле

(76.9)

то всегда будем подразумевать сказанное выше.

Если тензорное поле задано не во всей области , а лишь на некоторой поверхности (линии), то в уравнениях (7.9) нужно задавать, конечно, как функции параметров этой поверхности (линии). Тензорное поле может выродиться и в задание тензора в одной только точке М.

Вслед за преобразованием криволинейных координат происходит преобразование локального репера в каждой точке М, а значит, и преобразование координат тензора по обычному тензорному закону:

(7.10)

При этом, как мы видели, матрица совпадает с матрицей , а следовательно, обратная матрица - с матрицей :

=. (7.11)