Курсовая работа: Факторіальні кільця та їх застосування
№1 К–ідеал самого себе. Цей ідеал називається одиничним. Позначається Іе .
№2 Кожне кільце містить підкільце {0}, яке теж буде ідеалом кільця К. Цей ідеал називається нульовим. Позначається І0 .
Іе та І0 – тривіальні ідеали. В розумінні відношення включення Іе – найбільший, а І0 – найменший серед усіх ідеалів кільця.
Означення Ідеал І кільця К називається головним, якщо він складається з усіх елементів ка кільця К, аÎК, кÎК. Говорять, що він породжений елементом а. Позначають (а).
Наприклад, ідеал Z2 кільця Z буде головним, він породжений елементом 2 або –2.
2.1 Операції над ідеалами
Теорема Перетин ab ідеалів a, bÎK є ідеалом кільця K.
Доведення.
З того, що a, bÎI1 ÇI2 випливає, що abÎI1 , abÎI2 . Так як I1 та I2 –ідеали, то (a–b)ÎI1 , (a–b)ÎI2 Þ (a–b)ÎI1 ÇI2 . aÎI1 ÇI2 Þ aÎI1 , aÎI2 .
kÎK Þ kaÎI1 , kaÎI2 , kaÎI1 ÇI2 .
Отже, I1 ÇI2 ÎK.
Доведено.
Слід зауважити, що об’єднання ідеалів не завжди буде ідеалом кільця. Ця властивість поширюється на перетин n ідеалів.
Операції додавання й множення підмножин кільця можна, звичайно, застосувати до ідеалів.
Означення Сумою ідеалів I1 , I2 кільця K називається множина I1 +I2 , яка визначається рівністю
I1 +I2 ={a+bï aÎI1 , bÎI2 }.
Означення Добуток ідеалів I1 I2 кільця К теж буде ідеалом кільця К.
Нехай а і b – довільні ідеали кільця К.
Теорема 2 . Сума а + b ідеалів a і b кільця К є ідеал цього кільця.
Доведення.
Справді, сума (а1 +b1 ) + (a2 + b2 ) будь-яких двох елементів a1 +b1 і a2 +b2 множини a+b належить до a+b , оскільки (a1 +a2 )Îa , (b1 +b2 )Îb , і елемент – (а+b) = (–а) + (–b), протилежний довільно вибраному елементу (a+b)Î(a+b), також належить до a+b , бо (–a)Îa , (–b)Îb .
Отже, а + b є підгрупа адитивної групи кільця K . Крім того, для будь-яких елементів a+bÎa+b і хÎK x (a+b)=xa+xbÎa+b і (a+b) x=ax+bxÎa+b .
Цим теорему доведено.
Теорема 3. Добуток ab ідеалів а і b кільця К . також є ідеал кільця К .
Доведення.
Справді, сума 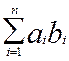 +
+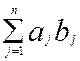 будь-яких двох елементів множини аb є, очевидно, елемент цієї самої множини, і елемент
будь-яких двох елементів множини аb є, очевидно, елемент цієї самої множини, і елемент 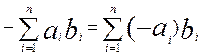 , протилежний довільно вибраному елементу
, протилежний довільно вибраному елементу  Îab , належить до ab . Крім того, для будь-яких
Îab , належить до ab . Крім того, для будь-яких
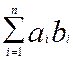 Îab і xÎK
Îab і xÎK ![]()
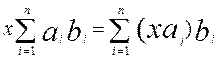 Îab й
Îab й 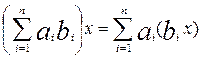 Îab .
Îab .
Цим теорему доведено.
Таким чином, у множині ідеалів кільця К здійсненні операції додавання й множення. Операція додавання ідеалів – асоціативна і комутативна, а операція множення – асоціативна. Якщо кільце К – комутативне, то операція множення ідеалів також комутативна.