№1

Нехай K₁ – підкільце кільця K. Довести, що K₁ ÇI –ідеал кільця K₁ .

Доведення.

Введемо позначення D=K₁ ÇI. Покажемо спочатку, що ідеал I, як і будь–який ідеал, містить нуль–елемент кільця K. Справді, оскільки I≠Ø, то в I існує хоч один елемент а. Тоді згідно з першим пунктом означення ідеалу, елемент а–а, тобто 0, теж належить ідеалу I. Оскільки 0ÎK₁ , 0ÎI, то 0ÎD і тому D≠Ø.

Якщо a, bÎD, то a, bÎK₁ і a, bÎI. Згідно з означенням ідеалу і критерієм підкільця, a±bÎI, a±bÎK₁ , а тому a±bÎD.

Нехай aÎD, bÎK₁ . Покажемо, що ab і ba належать D. Справді, оскільки DÍK₁ , то a, bÎK₁ і за критерієм підкільця K₁ маємо, що

ab, ba ÎK₁ . (1)

Оскільки DÍI, а I – ідеал кільця K, то для будь–якого елемента aÎDÍI і будь–якого елемента bÎK₁ ÎK маємо, що

ab, baÎI. (2)

З включень (1) і (2) випливає, що

ab, baÎK₁ ÇI=D.

Отже, D=K₁ ÇI –ідеал кільця K₁ .

Доведено.

№2

Чи є ідеалом (лівим або правим) така підмножина

в кільці M (2, Z).

Розв’язання

Перевіримо чи буде множина S лівим ідеалом

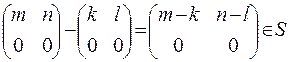
Перевіримо множення з ліва

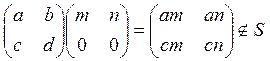
Отже, дана підмножина лівим ідеалом кільця M (2, Z).

Перевіримо чи буде правим ідеалом

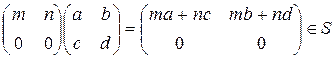
Отже правим ідеалом буде.

Відповідь: є правим ідеалом.

3. Факторіальні кільця

3.1 Кільця головних ідеалів та евклідові кільця

3.1.1 Подільність в області цілісності

В теорії кілець особливої уваги заслуговують кільця, які за своїми властивостями досить близькі до кільця цілих чисел. Зокрема, для цих кілець можна розвинути теорію подільності, аналогічну теорії подільності цілих чисел. Ці кільця дістали назву кілець головних ідеалів. Вивченням їх ми і будемо займатись. Але спочатку викладемо деякі загальні відомості, що стосуються подільності в області цілісності з одиницею.