Курсовая работа: Факторіальні кільця та їх застосування

Наведемо такі дві властивості нерозкладних елементів.

1. Якщо елемент рÎR нерозкладний, то і будь-який асоційований з ним елемент рε також нерозкладний. Ця властивість випливає з властивості 7 подільності елементів області цілісності R .

2. Якщо а – будь-який, а р – нерозкладний елемент з R , то або а ділиться на р, або а і р – взаємно прості.

Справді, якщо (а, р) = d, то d, як дільник нерозкладного елемента р, або є деякий дільник ε одиниці, або елемент вигляду рε. У першому випадку а і р взаємно прості, в другому – а ділиться на р.

Задачі

№1

Довести, що (-8+3)M (1+2) в кільці z [].

Доведення.

Поділимо ці гаусові числа, домноживши чисельник і знаменник частки на число спряжене із знаменником

.

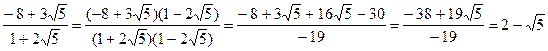Так як 2–ÎZ[], то (-8+3)M (1+2).

Доведено.

№2

Довести, що в області цілісності К елементи 25–17 і 7- асоційовані, якщо К=z[].

Доведення.

Асоційованість доводиться тим, що одне число ділиться на друге і навпаки.

Оскільки 3–2Î Z[], то (25–17)M(7-).

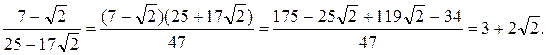
Бачимо, що і (7-)M(25–17).

Отже, дані елементи асоційовані.

Доведено.

№3

Довести, що характеристикою області цілісності є або нуль, або просте число.

Доведення.

Нехай K – область цілісності, а е – одиниця кільця К. Якщо me≠0 для жодного натурального числа m₁ , то характеристика кільця K дорівнює нулю.

Нехай тепер me=0 і m найменше натуральне число, що має цю властивість, тобто m – характеристика кільця K. Тоді m≠1, оскільки е≠0. Якщо m просте число, то твердження задачі доведено.

Нехай m складене число. Тоді існують натуральні числа s і t такі, що 1<s, t<m і m=st. Внаслідок комутативності кільця K маємо

0=me=(st) e=(se) (te).

Крім того, оскільки m – характеристика кільця K і s<m, t<m, то se≠0, te≠0 і тому (se) (te)=me≠0, бо K, як область цілісності, є кільцем без дільників нуля. Отже, ми прийшли до суперечності.