Курсовая работа: Идентификация параметра зазора при регулировании положения
Так как в электроприводе кроме двигателя имеется еще масса элементов, представляющих собой активно-индуктивную нагрузку (например, соединительные провода, щётки), то результирующая электромагнитная постоянная времени будет больше, чем Тя. Ориентировочно принимаем ![]() мс, т.е. в два раза больше Тя.
мс, т.е. в два раза больше Тя.
![]() ,
, ![]() .
.
Значит, дискретная передаточная функция цифрового электропривода будет иметь вид:
![]()

2 Синтез алгоритма регулятора скорости
2.1 Общие сведения
Синтез регулятора базируется на двух частотных характеристиках:
- дискретной частотной характеристике неизменяемой части привода ( ДЧХ НЧ)
- желаемой дискретной частотной характеристике
ДЧХ параметрически оптимизируемого регулятора определяется из соотношения:
 (2.1)
(2.1)
где ![]() - желаемая ДЧХ разомкнутого контура в области низких и средних частот.
- желаемая ДЧХ разомкнутого контура в области низких и средних частот.
 - характеризует запаздывание, связанное с дискретными операциями.
- характеризует запаздывание, связанное с дискретными операциями.
2.2 Определение дискретной частотной характеристики
неизменяемой части
Переход от дискретной передаточной функции к частотной характеристике проводится с помощью билинейного w-преобразования.
 (2.2)
(2.2)
 (2.3)
(2.3)
Заменяя в дискретной передаточной функции z на w и w на ![]() можно перейти к дискретной частотной характеристике
можно перейти к дискретной частотной характеристике
 (2.4)
(2.4)
Переход от z к w осуществляется с помощью этого выражения.
По выражению (1.7) можно записать:

![]() (2.5)
(2.5)
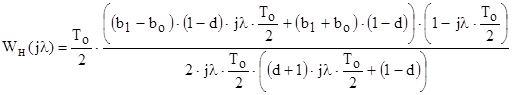 ,(2.6)
,(2.6)
![]() , (2.7)
, (2.7)
![]() , (2.8)
, (2.8)
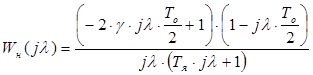 , (2.9)
, (2.9)
В нашем случае ![]() , тогда
, тогда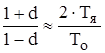 .
.
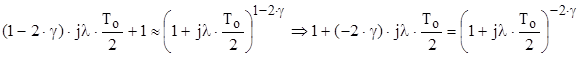
Окончательно получим ДЧХ неизменяемой части в виде:
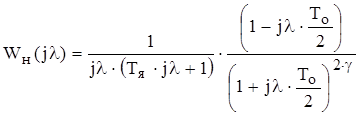 (2.10)
(2.10)
2.3 Определение желаемой дискретной частотной характеристики
Тип желаемой частотной характеристики зависит от требуемого порядка астатизма. Существует несколько видов типовых ЛЧХ цифровых электроприводов (чаще рассматривается пять видов типовых ЛЧХ). Все типовые ЛЧХ имеют в области средних частот асимптоты с наклоном -20дб/дек и отличаются друг от друга лишь наклоном в низкочастотной области. В области высоких частот формы ЛЧХ приняты одинаковыми. На рисунке 2.1 приведены пять типов желаемых ЛЧХ.