Курсовая работа: Идентификация параметра зазора при регулировании положения

; (4.5)

Реализуем данную функцию в MatLABe (см. рис. 4.3):

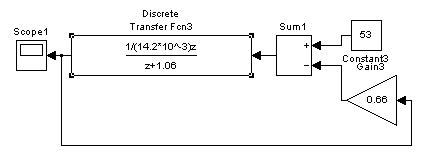
Рисунок 4.3 – Реализация подсистемы идентификации в MatLABe

Подсистема идентификации (ПИ) включается в систему управления следующим образом (см. рис. 4.4):

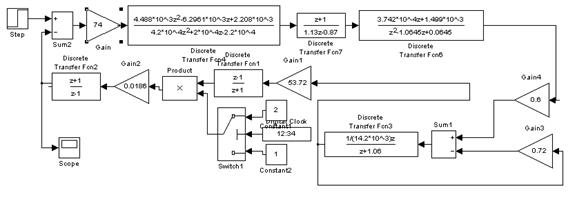
Рисунок 4.4 – Подключение ПИ в систему управления.

Исследуем переходные процессы в системах с ПИ и без нее при параметре момента инерции Jн =10Jд (см. рис. 4.5 и 4.6):

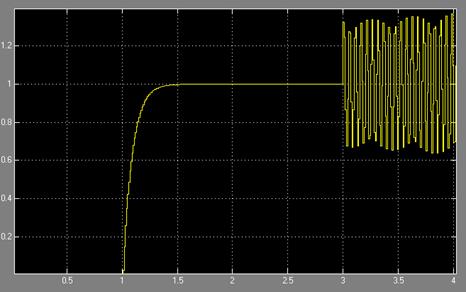
Рисунок 4.5 Переходные процессы без ПИ

W , м/с

t, c

W , м/с

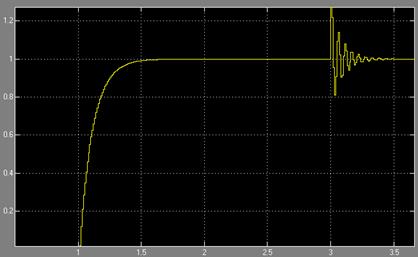
Рисунок 4.6 – Переходные процессы в системах с ПИ

Как видно из рисунка, уменьшилась колебательность системы, а также уменьшилась просадка скорости при изменении момента инерции нагрузки.

Действия ПИ аналогичны при моменте инерции нагрузки, равному 5Jд и Jд (см. рис. 4.7, 4.8):

t, c

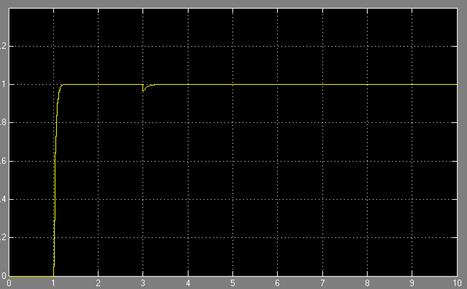
Рисунок 4.7 Переходные процессы при Jн =Jд без ПИ

t, c

W , м/с

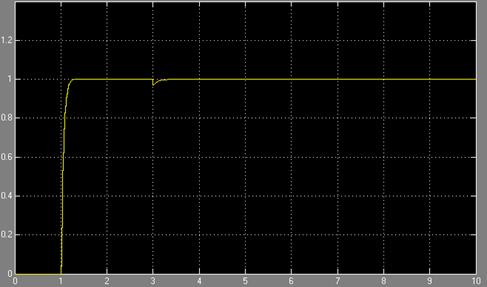
Рисунок 4.8 – переходные процессы при и Jн=Jд с ПИ

Предпримем попытку идентифицировать полученную систему, как апериодическое звено II порядка . При идентификации целесообразно использовать обратную частотную характеристику , точнее квадрат её модуля . Произведём замену , , а коэффициенты , , . В результате получим уравнение параболы .

Произведём ряд опытов с подачей в систему синусоидального воздействия единичной амплитуды и различной частоты.

м/с

рад/с

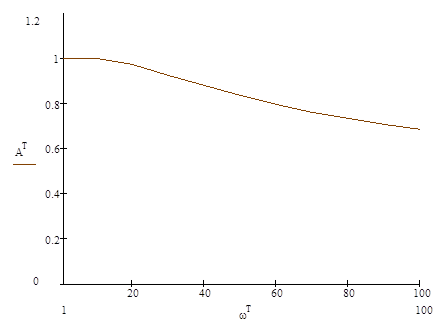
Рисунок 4.9 – Апмлитудно-частотная характеристика.

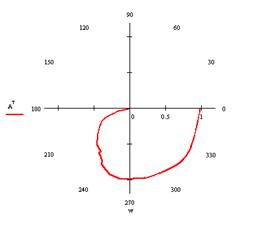
Рисунок 4.10 – Апмлитудно-фазовая характеристика.

В результате аппроксимации в параболу получили следующее уравнение:.

Отсюда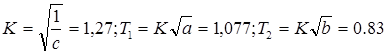

Тогда передаточная функция модели будет иметь вид:

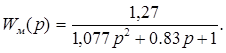
Преобразуем его в MathCADe в Z-форму

Реализуем полученную передаточную функцию в MATLAB 6