Курсовая работа: Инвариантность стационарного распределения трехузловой сети массового обслуживания
Список литературы
Введение
Математическая теория массового обслуживания является разделом теории случайных процессов, изучающим определенный класс задач, которые возникают на практике, когда заявки, нуждающиеся в обслуживании, прибывают к некоторому обслуживающему устройству. В качестве примеров заявок и обслуживающих их устройств можно назвать абонентские вызовы, поступающие на телефонный коммутатор, станки, ожидающие обслуживание рабочими, автомобили, ожидающие у дорожного пересечения, самолёты, прибывающие в аэропорт, суда, заходящие в порт и т.д.
Системами (моделями) массового обслуживания называют математические модели систем, которые предназначены для обслуживания заявок, поступающих через случайные промежутки времени, причем длительность обслуживания в общем случае также случайна.
Системы массового обслуживания описываются заданием:
входящего потока заявок;
совместного распределения времен обслуживания заявок;
числа обслуживающих приборов (линий);
дисциплины обслуживания, организации очереди и процесса обслуживания.
В данной курсовой работе рассматривается система массового обслуживания для которой:
1) входящий поток заявок является пуассоновским;
2) в системе три обслуживающих прибора;
A) Марковский случай.
3 время обслуживания экспоненциальное
4 дисциплина обслуживания FIFO;
Б) Немарковский случай.
3) время обслуживания определяется с помощью произвольной функцией распределения времени ![]() обслуживания
обслуживания ![]() -м прибором одной заявки, такой что
-м прибором одной заявки, такой что
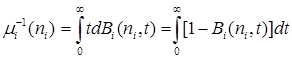 ;
;
4) дисциплина обслуживания LCFSPR; (заявка, поступающая в ![]() -ый узел, вытесняет заявку с прибора и начинает обслуживаться, вытесненная заявка идет в начало очереди).
-ый узел, вытесняет заявку с прибора и начинает обслуживаться, вытесненная заявка идет в начало очереди).
В курсовой работе для открытой марковской сети массового обслуживания составим уравнения равновесия, найдем стационарные вероятности, установим условия эргодичности. Для не марковского случая составим дифференциально-разностное уравнение в частных производных для процесса, дополненного остаточными временами, найдем решение данного уравнения. Сравним марковский и немарковский случай. Сделаем вывод.
1. Теоретические сведения
1.1 Марковские процессы
Пусть Т и Х - некоторые подмножества числовой прямой R.
Определение 1. Случайный процесс ![]() со значениями в Х называется марковским, если для любых
со значениями в Х называется марковским, если для любых ![]() из Т и любых борелевских множеств
из Т и любых борелевских множеств ![]() из R
из R
![]()
Другими словами, марковский процесс это такой случайный процесс, у которого при фиксированном настоящем будущее не зависит от прошлого. Если Х={i} конечно или счётно, то марковский процесс называют цепью Маркова. Если вероятности
![]()
не зависят от s , а зависят от t , то цепь Маркова называется однородной. Цепь Маркова с T={0,1,2,... } называют цепью с дискретным временем, цепь Маркова c
![]()
называют цепью с непрерывным временем.
Обозначим
![]()