Курсовая работа: Инвариантность стационарного распределения трехузловой сети массового обслуживания
2.2 Сеть массового обслуживания
Дана открытая марковская сеть массового обслуживания, состоящая из трех подсистем. Состояние сети в момент времени t определяется вектором
число заявок в i -ой подсистеме в момент времени t . Входящий поток является пуассоновским потоком с параметром 
. Времена обслуживания заявок в i -ой системе массового обслуживания распределены по показательному закону с параметром 
, зависящим от текущего числа заявок в i -ой системе, i =1,2,3.
Заявки поступают из общего потока заявок во второй узел и первый узел с вероятностями 
и 
соответственно. После обслуживания во втором узле заявки поступают на третий узел. А после обслуживания на первом узле заявки поступают с вероятностью 
в третий узел либо с вероятностью 
в первый узел, либо с вероятностью в третий узел. После обслуживания на 3 узле заявки уходят из системы.
2.3 Уравнения равновесия
Предположим, что существует стационарное распределение
. Составим уравнение равновесия.
P
P
+
P
+
+
P
+
P
+
+
P
+ 
P 
+
+
P
2.4 Нахождение стационарных вероятностей
Для того, чтобы найти решение уравнения равновесия , воспользуемся теоремой 1 из 1.7 из которой получим, что
,
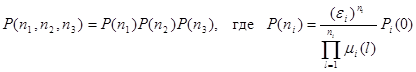-вероятность поступления заявок в i -ую подсистему.
Таким образом, нам необходимо найти 
. Для этого воспользуемся соотношением (3) из 1.7
Из системы 
получим
где 
-вероятности перехода
Матрица перехода имеет вид:
Тогда, получим
где Io - нулевой вектор.
Итак, стационарное распределение найдено с точностью до постоянного множителя P ( Io).
2.5 Условия эргодичности
Для исследования эргодичности применим эргодическую теорему Фостера (теорема 1 из 1.1)
Теорема (Эргодическая теорема Фостера).
Регулярная Марковская цепь с непрерывным временем и счетным числом состояний эргодична, если она неприводима и система уравнений
