Курсовая работа: Итерационные методы решения систем нелинейных уравнений

Для полноты представления о методах нахождения решения системы необходимо разъяснить такое понятие, как "скорость сходимости". Если для последовательности x_n , сходящейся к пределу х_* , верна формула

(k - положительное действительное число), то k называется скоростью сходимости данной последовательности.

2. Итерационные методы решения систем нелинейных уравнений

2.1 Метод простых итераций

Метод простых итераций (последовательных приближений) является одним из основных в вычислительной математике и применяется для решения широкого класса уравнений. Приведём описание и обоснование этого метода для систем нелинейных уравнений вида

f_i (x₁ ,x₂ ,...x_n ) = 0, i =1,2,..n ;

Приведём систему уравнений к специальному виду:

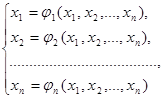(2.1)

Или в векторном виде . (2.2)

Причем переход к этой системе должен быть только при условии, что

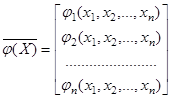является сжимающим отображением.

Используя некоторое начальное приближение X⁽⁰⁾ = (x₁ ⁽⁰⁾ ,x₂ ⁽⁰⁾ ,...x_n ⁽⁰⁾ )

построим итерационный процесс X^(k+1) =  (X^{(k )} ). Расчёты продолжаются до выполнения условия . Тогда решением системы уравнений является неподвижная точка отображения .

Проведём обоснование метода в некоторой норме пространства .

Приведём теорему о сходимости, выполнение условий которой приводит к нахождению решения системы.

Теорема (о сходимости). Пусть

1). Вектор-функция Ф(х) определена в области

;

2). Для выполняется условие

3). Справедливо неравенство

Тогда в итерационном процессе:

1.

2. ,

где – решение системы уравнений;

3. ,

Замечание. Неравенство условия 2) есть условие Липшица для вектор -функции Ф(х) в области S с константой (условие сжатия). Оно показывает, что Ф является оператором сжатия в области S , т. е. для уравнения (2.2) действует принцип сжатых отображений. Утверждения теоремы означают, что уравнение (2.2) имеет решение в области S , и последовательные приближения сходятся к этому решению со скоростью геометрической последовательности со знаменателем q .