Курсовая работа: Итерационные методы решения систем нелинейных уравнений

Рассмотрим систему уравнений

в предположении, что – непрерывно-дифференцируемые функции.

Полагая

,

прейдём к векторной записи

(3.1)

Опишем общий шаг метода. Пусть уже получено приближение проведём линеаризацию вектор-функции в окрестности точки - разложим функцию в ряд Тейлора, оставив только два первых члена в силу малости отклонения приближения от корня:

.

Здесь 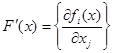– матрица Якоби для вектор-функции .

Очередное приближение определяется как решение линейной системы , т.е.

Если матрица Якоби не вырожденна, то решение системы линейной системы можно записать в явном виде, что приводит к стандартной формуле метода Ньютона

(3.2)

Таким образом, в основе метода Ньютона лежит идея линеаризации вектор-функции в окрестности каждого приближения (на каждой итерации), что позволяет свести решение системы (3.1) к последовательному решению линейных систем.

Через уже известное приближение к корню можно записать, что , где . Тогда после линеаризации получим систему уравнений, линейную относительно . Таким образом, на каждом шаге мы будем находить приращения , и новое приближение к решению по формулам:

– система линейных уравнений

Рассмотрим вопрос о сходимости метода Ньютона. Точное условие сходимости метода Ньютона для решения систем нелинейных уравнений имеет довольно сложный вид. можно отметить очевидный результат: в достаточно малой окрестности корня итерации сходятся, если матрица Якоби невырожденная, причём сходимость квадратичная.

Приведём ряд теорем, выполнение условий которых должно обеспечивать сходимость метода Ньютона.

Пусть в пространстве выбрана некоторая векторная норма и согласованная с ней матричная норма .

Теорема (о сходимости). Пусть

1) вектор-функция определена и непрерывно-дифференцируема в области

где – решение уравнения (3.1),

2) для всех существует обратная матрица , причём

3)для всех