Курсовая работа: Итерационные методы решения систем нелинейных уравнений

(2.3)

Будем рассуждать по индукции. При утверждение справедливо, т.к. и . Допустим, что приближения принадлежат S, и неравенство (2.3) выполнено для . Поскольку , то для с учётом условия 2) теоремы имеем

.

По индуктивному предположению

.

Следовательно,

,

т.е. неравенство (2.3) справедливо для . Покажем, что . Учитывая свойство (2.3) при , получаем

Итак, , и первое утверждение теоремы доказано.

Покажем, что последовательность является сходящейся. С этой целью проверим признак сходимости Коши (покажем, что последовательность является фундаментальной).

По аналогии с предыдущим для любых р =1,2,… имеем

Поскольку , то , поэтому для найдётся такой номер , что для будет

Это означает выполнение признака Коши, что гарантирует сходимость последовательности . Обозначим . Утверждение 2) теоремы доказано.

Для доказательства последнего утверждения воспользуемся полученным выше неравенством

Перейдём здесь к пределу при . Учитывая непрерывность функции и тот факт, что , получаем требуемый результат – утверждение 3).

Замечание 2. В условиях теоремы решение уравнения (2.2) в области S является единственным.

Действительно, пусть имеются два решения , причём . Тогда

,

Получили противоречие, что и требовалось доказать.

Обсудим условие 2) доказанной теоремы. Рассмотрим уравнение (2.2) в покомпонентной записи

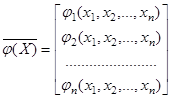
и предположим, что функции непрерывно-дифференцируемы в области S (т.е. существуют и непрерывны в S частные производные

).

Теперь выясним достаточное условие выполнения неравенства 2) в этом случае.

Образуем матрицу Якоби системы функций