Курсовая работа: Итерационные методы решения систем нелинейных уравнений

Содержание

1. Методы решения систем нелинейных уравнений. Общая информация

2. Итерационные методы решения систем нелинейных уравнений

2.1 Метод простых итераций

2.2 Преобразование Эйткена

2.3 Метод Ньютона

2.3.1 Модификации метода Ньютона

2.3.2 Квазиньютоновские методы

2.4 Другие итерационные методы решения систем нелинейных уравнений

2.4.1 Метод Пикара

2.4.2 Метод градиентного спуска

2.4.3 Метод релаксаций

3. Реализация итерационных методов программно и с помощью математического пакета Maple

3.1 Метод простых итераций

3.2 Метод градиентного спуска

3.3 Метод Ньютона

3.4 Модифицированный метод Ньютона

Выводы

Список использованной литературы

1. Методы решения нелинейных уравнений. Общая информация.

Пусть нам дана система уравнений, где - некоторые нелинейные операторы:

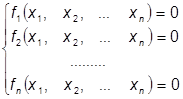(1.1)

Она может быть также представлена в матричном виде:

(1.1)

Где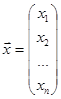

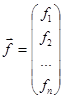
Её решением называется такое значение , для котрого

Очень распространенной является вычислительная задача нахождения некоторых или всех решений системы (1.1) из n нелинейных алгебраических или трансцендентных уравнений с n неизвестными.

Обозначим через Х вектор-столбец (х ₁ , х ₂ ,..., х_n )^T и запишем систему уравнений в виде формулы (1.2): F (Х ) = 0, где F = (f ₁ , f ₂ ,..., f_n )^T .

Подобные системы уравнений могут возникать непосредственно, например, при конструировании физических систем, или опосредованно. Так, к примеру, при решении задачи минимизации некоторой функции G (х )часто необходимо определить те точки, в которых градиент этой функции равен нулю. Полагая F = grad G, получаем нелинейную систему.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--