Курсовая работа: Итерационные методы решения систем нелинейных уравнений

Тогда метод Ньютона (3.2)

1)

2)

3)

Доказательство. Докажем первое утверждение теоремы с помощью индукции. По условию . Допустим, что . Поскольку , то . Рассмотрим условие 3) теоремы для

.

Согласно формуле (3.2)

,

Кроме того . Тогда предыдущее неравенство принимает вид

Следовательно,

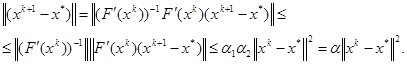
Таким образом, имеет место неравенство

(3.3)

По предположению индукции . Поскольку в силу условия 4)

, то

Это значит, что для , и шаг индукции реализован. Превое утверждение теоремы доказано.

Продолжим доказательство. Положим перепишем оценку (3.3) после умножения на в виде . Покажем, что

(3.4)

Будем рассуждать по индукции. При неравенство (3.4.) очевидно. Допустим, что оно справедливо для некоторого . Тогда

Переход завершен, т.е. неравенство (3.4) справедливо для всех . Перепишем его в исходных обозначениях

Получили утверждение 3). При этом

, т.е. .

Это значит, что имеет место сходимость:

Замечание 1. Неравенство (3.3) при условии означает, что последовательность сходится к решению сквадратичной скоростью.

Замечание 2. Поскольку , то из утверждения 3) следует оценка погрешности метода Ньютона