что и требовалось доказать.

Следствие. Мера открытого ограниченного множества G есть точная нижняя граница мер всевозможных открытых ограниченных множеств, содержащих G .

Теорема 2 . Если открытое ограниченное множество G является суммой конечного числа или счетного множества взаимно не налегающих открытых множеств

,

то

.

Это свойство меры называется полной аддитивностью .

Д о к а з а т е л ь с т в о. Пусть (i = 1, 2, …) суть составляющие интервалы множества G_k . Покажем, что каждый из них является составляющим интервалом суммы G.

В самом деле, то обстоятельство, что G, очевидно. Остается убедиться, что концы интервала не принадлежат G. Допустим, что, например, правый конец интервала принадлежит G. Тогда этот правый конец (обозначим его через m) должен принадлежать какому-нибудь из слагаемых множеств. Пусть m Î G_{k '} . (Очевидно k¢ ¹ k, ибо множеству G_k точка m заведомо не принадлежит.) Но множество G_{k ¢} открыто и, стало быть, точка m принадлежит одному из составляющих интервалов этого множества m Î d_{i ¢} ^{( k} ¢⁾ . Однако это влечет за собой то, что интервалы d_i ^{( k )} и d_{i ¢} ^{( k} ¢⁾ пересекаются, последнее же противоречит условию G_k G_{k ¢} = 0.

Итак, действительно, каждый из d_i ^{( k )} есть составляющий интервал множества G. С другой стороны, каждая точка G принадлежит хоть одному d_i ^{( k )} . Наконец, все эти интервалы различны. Таким образом, множество

(i = 1, 2, …; k = 1, 2, …)

есть множество всех составляющих интервалов суммы G.

Установив это, уже легко закончить доказательство:

=

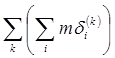
что и требовалось доказать.

Для того чтобы перенести теорему (соответственно изменить ее) на случай суммы п е р е с е к а ю щ и х с я слагаемых, нам понадобятся две простые леммы.

Лемма 2. Пусть сегмент [P, Q] покрыт конечной системой Н интервалов (l, m ). Тогда

Д о к а з а т е л ь с т в о. Выделим из системы Н некоторую ее часть Н*, которая строится следующим образом: обозначим через (l_{1 ,} ) какой-нибудь из интервалов системы H, содержащих точку P

l₁ < P < m₁

(хоть один такой интервал существует). Если окажется, что m₁ >Q, то интервал (l_1, m₁ ) , и составляет требуемую систему H^* . Если же m₁ Q, то m₁ Î[P, Q], и можно в системе H найти интервал ( l₂ ,m₂ ), содержащий точку m_{1 ,}

l₂ < m₁ < m₂

Если окажется, что m₂ >Q, то процесс окончен, и интервалы (l_1, m₁ ) и ( l₂ ,m₂ ) и составляют систему Н*.

Если же m₂ Q, то m₂ Î[P, Q], и можно в системе H найти интервал ( l₃ ,m₃ ), содержащий m₂ .

l₃ < m₂ < m₃

Если m₃ >Q, то процесс закончен, а если m₃ Q, то продолжаем наш процесс.

Но ведь множество H по условию конечно, а наш процесс состоит в выделении из H все новых и новых интервалов, ибо

m₁ < m₂ < m₃ < …

Поэтому процесс обязательно должен закончится, а конец его состоит в том, что какая-то из точек m_k окажется лежащей правее точки Q.

Пусть m_n >Q, но m_{n -1} £Q, т.е. процесс заканчивается после n-го шага.

Тогда интервалы (l_1, m₁ ), ( l₂ ,m₂ ), … , (l_{n ,} m_n ) и составляют систему H. При этом l_{k +1} <m_k (k = 1, 2, … , n-1).

Значит

а так как m_n - l₁ > Q – P, то Q – P<, откуда и подавно

Q – P<.

Лемма 3. Пусть интервал D есть сумма конечного или счетного множества открытых множеств

D = .

Тогда

mD.

Д о к а з а т е л ь с т в о. Пусть D = (A, B) и пусть составляющие интервалы множества G_k суть d_i ^{( k )} (i = 1, 2, …).

Возьмем положительное число e (0 < e < ) и рассмотрим сегмент , содержащийся в интервале D.

Этот сегмент покрыт системой интервалов d_i ^{( k )} (i = 1, 2, …; k = 1, 2, …). Применяя к этой системе теорему Бореля о конечном покрытии из § 2, гл. II, мы получим некоторую конечную систему

(s = 1, 2, … n),