Так как число e произвольно мало, то

B – A,

и лемма доказана.

Теорема 3. Если открытое ограниченное множество G является суммой конечного числа или счетного множества открытых множеств G_k , G = , то

mG.

Д о к а з а т е л ь с т в о. Пусть D_i (i = 1, 2, …) суть составляющие интервалы суммы G. Тогда mG = .

Но откуда, в силу леммы 3, и, стало быть,

(*)

С другой стороны

При этом (что является здесь основным) отдельные слагаемые правой части взаимно не пересекаются (потому что при i¹i`). Значит, мы находимся в условиях применимости теоремы 2, а потому

(**)

Сопоставляя (*) и (**), мы и получаем теорему.

Мера ограниченного замкнутого множества

Пусть F непустое ограниченное замкнутое множество и S наименьший сегмент, содержащий множество F. Как известно, множество C_S F открыто и поэтому имеет определенную меру m[C_S F]. Это дает возможность установить следующее определение.

Определение 1 . Мерой непустого ограниченного замкнутого множества F называется число

где S=[A, B] есть наименьший сегмент, содержащий множество F.

Для пустого замкнутого множества меру определять не нужно, ибо такое множество открыто и мерой его мы уже условились считать число 0. Кроме того, непустое замкнутое ограниченное множество не может оказаться открытым множеством, так что нет надобности ставить вопрос о связи определений меры открытого и замкнутого множества.

Рассмотрим некоторые примеры.

1. F=[a, b]. В этом случае, очевидно, S=[a, b] и C_s F=0, так, что m [a, b] = b – a, т. е. мера сегмента равна его длине.

2. F есть сумма конечного числа попарно не пересекающихся сегментов

Можно считать, что сегменты перенумерованы в порядке возрастания левых концов; тогда, очевидно,

(k=1, 2, … n-1),

откуда следует, что

Стало быть,

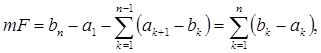
т.е. мера суммы конечного числа попарно не пересекающихся сегментов равна сумме длин этих сегментов .

3. Пусть (Канторово совершенное множество). В этом случае

и откуда

т.е. Канторово совершенное множество имеет меру нуль . Этот факт интересно сопоставить с тем, что мощность множества есть с.

Теорема 1. Мера ограниченного замкнутого множества F не отрицательна.

Д о к а з а т е л ь с т в о. Действительно, если пользоваться обозначениями определения 1, то очевидно Ì (А, В), и по теореме 1, откуда и следует, что

Лемма . Пусть F ограниченное замкнутое множество, содержащееся в интервале D, тогда

D- [ C_D F]

Д о к а з а т е л ь с т в о. Множество C_D F – открыто, так что лемма имеет смысл. Пусть D=(A, B), а наименьший сегмент, содержащий множество F, есть S=[a, b] (рис.1.).

Тогда легко видеть, что С_D F=C_D S+C_s F.

Рис. 1

Оба слагаемые правой части открыты и взаимно не налегают. Значит, по свойству аддитивности меры (теорема 2) будет m[C_D F]=m[C_D S]+m[C_s F].