Д о к а з а т е л ь с т в о вытекает из следующей цепи неравенств:

Доказанное свойство меры называется ее полной аддитивностью.

В последней теореме существенно было, что отдельные слагаемые попарно не пересекаются. Избавимся от этого ограничения, пока, впрочем, для случая конечного числа слагаемых множеств.

Теорема 5. Сумма конечного числа измеримых множеств есть измеримое множество.

Д о к о з а т е л ь с т в о. Пусть причем множества

E_k (k =1, 2, …, n) измеримы.

Возьмем произвольное e>0 и построим для каждого k такое замкнутое множество F_k и такое открытое ограниченное множество G_k , чтобы было

F_k ÌE_k ÌG_k , mG_k – mF_k < (k = 1, 2, …, n).

Сделав это, положим

Очевидно, что множество F замкнуто, а G открыто и ограничено, и что

FÌEÌG, откуда следует, что

mF£m_* E£m^* E£mG. (^* )

Но множество G – F открыто (ибо его можно представить в форме

G·CF) и ограничено. Значит, это множество измеримо. Множество F также измеримо, а потому, поскольку

G = F + (G – F)

и множества F и G – F не пересекаются, можно применить предыдущую теорему, что дает mG = mF + m(G – F), откуда

m(G – F) = mG – mF.

Аналогично мы установим, что

m(Gk – Fk) = mGk – mFk (k = 1, 2, …, n).

Отметим теперь легко проверяемое включение

G-F(G_k -F_k ).

Все входящие сюда множества открыты и ограничены, так что, на основании теорем § 1, мы имеем

m(G-F)

или

mG - mF<e.

Отсюда и из (*) вытекает, что m*E - m_* E<e, а также как e сколь угодно мало, то

m*E = m_* E.

Теорема 6. Пересечение конечного числа измеримых множеств измеримо.

Д о к а з а т е л ь с т в о. Пусть E=, причем множества E_k измеримы. Назовем через D какой-нибудь интервал, содержащий все множества E_k . Легко проверить, что C_D E=.

Но множества СE_k измеримы одновременно с множествами E_k , откуда, в силу теоремы 5, следует измеримость множества C_D E, а с ним и множества E, что и требовалось доказать.

Теорема 7. Разность двух измеримых множеств измерима.

Д о к а з а т е л ь с т в о. Пусть E = E₁ - E₂ , где множества E₁ и E₂ измеримы. Назовем через D какой-нибудь интервал, содержащий оба множества E₁ и E₂ . Тогда E=E₁ ·C_D E₂ и дело сводится к предыдущей теореме.

Теорема 8. Если в условиях теоремы 7 будет E ₁ E ₂ , то

ME = mE₁ - mE₂ .

Д о к а з а т е л ь с т в о. Очевидно E₁ =E+E₂ (EE₂ =0), откуда, в силу теоремы 4, mE₁ =mE+mE₂ , что равносильно теореме.

Теорема 9. Если ограниченное множество E является суммой счетного множества измеримых множеств, то E измеримо.

Д о к а з а т е л ь с т в о. Пусть E=.

Введем множества A_k (k=1, 2, …), полагая

A₁ =E₁ , A₂ =E₂ -E₁ , …, A_k =E_k -(E₁ +…+E_k-1 ), …

Легко проверить, что . При этом все множества A_k измеримы и попарно не пересекаются (в последнем вся суть доказательства), так что дело свелось к теореме 4.

Условие ограниченности множества Е (которое в теореме 5 выполнялось само собой) отбросить нельзя, как видно хотя бы из примера Е_k = [0, k], где сумма _k = [0, +) неизмерима.

Теорема 10. Пересечение счетного множества измеримых множеств измеримо.

Д о к а з а т е л ь с т в о. Пусть 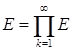_k , где все множества Е_k измеримы. Так как ЕЕ₁ , то множество Е ограничено. Обозначим через D какой-нибудь интервал, содержащий это множество, и положим А_k = D Е_k (k=1, 2, 3, …).

Тогда

_k =_k )=_k .