Курсовая работа: Измеримые множества

В заключение установим две теоремы, играющие важную роль в теории функций.

Теорема 11. Пусть множества Е₁ , Е₂ , Е₃ , … измеримы. Если

и если сумма 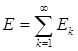ограничена, то

[mE_n ].

Д о к а з а т е л ь с т в о. Легко видеть, что множество Е можно представить в форме

Е=Е₁ + (Е₂ – Е₁ ) + (Е₃ – Е₂ ) + (Е₄ – Е₃ ) + …,

где отдельные слагаемые попарно не пересекаются. Отсюда, в силу теорем 4 и 8, следует, что

На основании самого определения суммы бесконечного ряда, последнее равенство можно переписать так

{

а это равносильно теореме, ибо

mE₁ + =mE_n

Теорема 12. Пусть E ₁ , E _2, E ₃ ,… суть измеримые множества, и Е= . Если Е₁ É E₂ É E₃ É _…, то

mE = lim .

Д о к а з а т е л ь с т в о . Эту теорему легко свести к предыдущей. Действительно, обозначив через D какой-нибудь интервал, содержащий множество Е₁ , мы будем иметь

С_D E₁ ÌC_D E₂ ÌC_D E₃ Ì ..., C_D E=.

В силу теоремы 11 мы получаем, что

m(С_D E)=

что можно представить и так:

mD - mE=

а это равносильно теореме.

Измеримость и мера как инварианты движения

Пусть даны два множества А и В, состоящие из объектов любой природы. Если указано правило, которое каждому элементу а множества А ставит в соответствие один и только один элемент b множества В, то говорят, что установлено однозначное отображение множества А в множество В. При этом не предполагается, что каждый элемент множества В оказываетс