Курсовая работа: Метод Рунге-Кутты четвертого порядка с автоматическим выбором шага интегрирования решения задачи Коши

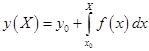. (2.2.1)

В качестве примера можно рассмотреть первую квадратурную формулу Гаусса, также называемую «правилом средней точки»:

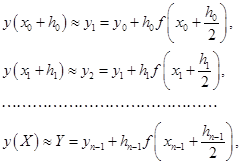(2.2.2)

где и – граничные точки подинтервалов, на которые разбит интервал интегрирования. Известно, что оценка глобальной погрешности этой формулы имеет вид . Таким образом, если желаемая точность составляет 6 десятичных знаков, ее обычно можно получить приблизительно за 1000 шагов, то есть этот метод в тысячу раз быстрее. Поэтому Рунге поставил следующий вопрос: нельзя ли распространить этот метод на исходную задачу Коши? Первый шаг длины должен иметь вид

. (2.2.3)

Но какое значение взять для ? За неимение лучшего естественно использовать один малый шаг метода Эйлера длины . Тогда из предыдущей формулы получим:

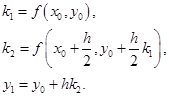(2.2.4)

Решающим обстоятельством здесь является умножение в третьем выражении на , в результате чего влияние погрешности становится менее существенным. Точнее, вычислим для разложение Тейлора по степеням :

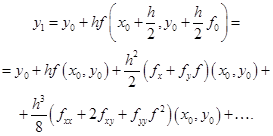(2.2.5)

Его можно сравнить с рядом Тейлора для точного решения, который получается из того, что путем повторного дифференцирования с заменой на каждый раз, когда оно появляется:

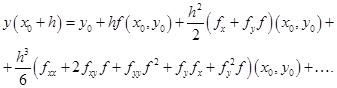(2.2.6)

Вычитая из последнего равенства предыдущее, получим для погрешности первого шага выражение

(2.2.7)

Таким образом, если все частные производные второго порядка ограничены, то

.

Чтобы получить приближенное значение решения исходной задачи в конечной точке , будем применять формулы (2.2.4) последовательно к интервалам . Приведенные выше формулы являются усовершенствованным методом Эйлера. Для вычислений с высокой точностью, однако, следует пользоваться другими методами, одним из которых как раз является метод Рунге-Кутты.

1.3 Общая формулировка методов Рунге-Кутты

Рунге и Хойн построили новые методы, включив в указанные формулы один или два добавочных шага по Эйлеру. Но именно Кутта сформулировал общую схему того, что теперь называется методом Рунге-Кутты.

Пусть – целое положительное число (число стадий, этапов) и – вещественные коэффициенты. Тогда метод

(2.3.1)

называется -стадийным явным методом Рунге-Кутты для исходной задачи Коши (2.1.1)

Обычно коэффициенты удовлетворяют условиям

. (2.3.2)

Эти условия были приняты Куттом без каких-либо комментариев. Смысл их заключается в том, что все точки, в которых вычисляется , являются приближениями первого порядка к решению. Эти условия сильно упрощают вывод условий, определяющих порядок аппроксимации для методов высокого порядка. Однако для методов низких порядков эти предположения необходимыми не являются.

Метод Рунге-Кутты имеет порядок , если для достаточно гладких задач (2.1.1) справедливо неравенство

, (2.3.3)

то есть ряды Тейлора для точного решения и для совпадают до члена включительно.

После статьи Бутчера вошло в обычай символически представлять метод (2.3.1) по средствам следующей таблицы:

« 1 2 3 4 5 6 7 8 9 10 » К-во Просмотров: 504 Бесплатно скачать Курсовая работа: Метод Рунге-Кутты четвертого порядка с автоматическим выбором шага интегрирования решения задачи Коши >>> Скачать <<< Меню Поиск