Курсовая работа: Метод Рунге-Кутты четвертого порядка с автоматическим выбором шага интегрирования решения задачи Коши

Со времен работы Лагранжа и особенно Коши всякий установленный численно результат принято сопровождать надежной оценкой погрешности. Лагранж дал известные оценки погрешности многочленов Тейлора, а Коши вывел оценки для погрешности метода ломаных Эйлера. Через несколько лет после первых успехов методов Рунге-Кутты также пришел к заключению, что для этих методов нужны оценки погрешностей[2] .

1.7.1 Строгие оценки погрешности

Способ, которым Рунге получил оценку погрешности, делаемой на одном шаге («локальной погрешности»), может быть описан следующим образом. Для метода порядка рассмотрим локальную погрешность

(2.7.1)

и воспользуемся ее тейлоровским разложением:

, (2.7.2)

где и . Явное вычисление дает выражение вида

, (2.7.3)

где и содержат частные производные до порядков и соответственно. Далее поскольку , имеем . Таким образом, если ограничены все частные производные до порядка включительно, имеем и . Следовательно, существует постоянная такая, что и

. (2.7.4)

Бибербах использовал несколько иной подход. Запишем

(2.7.5)

и воспользуемся тейлоровскими разложениями

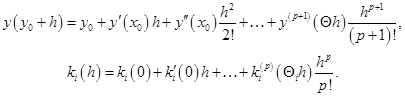(2.7.6)

Для векторных функций эти формулы справедливы покомпонентно (возможно, с различным ). В силу условий порядка первые члены разложения (2.6.5) по степеням обращаются в нуль. Таким образом, справедлива следующая теорема.

Теорема.

Если метод Рунге-Кутты (2.3.1) имеет порядок и если все частные производные до порядка включительно существуют и непрерывны, то локальная погрешность метода (2.3.1) допускает следующую строгую оценку:

, (2.7.7)

или

. (2.7.8)

Продемонстрируем этот результат, применяя к скалярному дифференциальному уравнению первый метод Рунге-Кутты (2.2.4), который имеет порядок . Дифференцируя (2.1.1), получим

. (2.7.9)

Вторая производная величины имеет вид

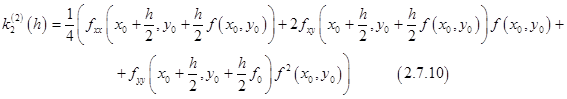
Если условия теоремы выполнены, то легко видеть, что выражения (2.7.9) и (2.7.10) ограничены постоянной, которая не зависит от , что и дает оценку (2.7.8).

1.7.2 Главный член погрешности

Для методов высших порядков строгие оценки погрешностей, подобные (2.7.7), становятся очень непрактичными. Поэтому гораздо более реалистично рассматривать первый ненулевой член в тейлоровским разложении погрешности.

Теорема.

Если метод Рунге-Кутты имеет порядок и если непрерывно дифференцируема раз, то для главного члена погрешности имеем: