Курсовая работа: Метод Рунге-Кутты четвертого порядка с автоматическим выбором шага интегрирования решения задачи Коши

(2.7.12)

1.7.3 Оценка глобальной погрешности

Глобальной (накопленной) погрешностью[3] называется погрешность численного решения после выполнения нескольких шагов. Пусть мы имеем некоторый одношаговый метод, с помощью которого при заданных начальных данных и длине шага мы определяем численное решение , аппроксимирующее . Воспользуемся обозначениями Хенричи для этого процесса:

, (2.7.13)

и назовем функцией приращения для данного метода.

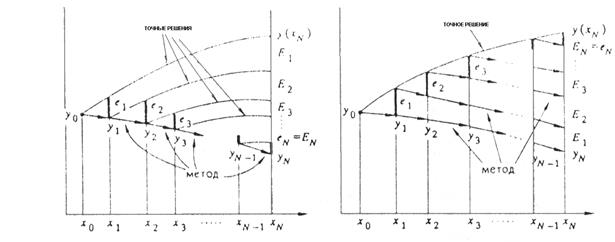
Оценивание глобальной погрешности методами a ) и b )

Тогда численное решение в точке получается с помощью пошаговой процедуры

, (2.7.14)

и наша задача состоит в оценке глобальной погрешности

(2.7.15)

Эта оценка находится простым способом: локальные погрешности переносятся в конечную точку и затем складываются. Этот «перенос погрешностей» можно выполнить двумя разными способами:

a) перенося погрешность вдоль кривых точных решений; этот способ может дать хорошие результаты, если известны хорошие оценки распространения погрешности для точных решений.

b) перенося погрешность -го шага посредством выполнения шагов численного метода; этот способ использовали в своих доказательствах Коши (1824) и Рунге (1905), он легко обобщается на многошаговые методы.

В обоих случаях оценим сначала локальные погрешности:

. (2.7.16)

Займемся теперь оценкой перенесенных погрешностей .

a) Теорема.

Обозначим окрестность точки , где – точное решение уравнения

.

Пусть в справедливы оценки локальных погрешностей (2.7.16) и выполнено одно из условий:

или . (2.7.17)

Тогда имеет место следующая оценка глобальной погрешности (2.7.15):

, (2.7.18)

где ,

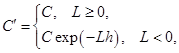
и достаточно мало для того, чтобы численное решение оставалось в .

Доказательство.

При оценка (2.7.18) переходит в .