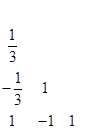Курсовая работа: Метод Рунге-Кутты четвертого порядка с автоматическим выбором шага интегрирования решения задачи Коши
Далее последний столбец 
не может быть нулевым, так как из того, что 
, следует
в силу условия h). Таким образом, из последней леммы следует, что 
. Последнее тождество 
вытекает из равенства 
, которое является следствием условий a) и b).
Теорема .
Если выполнены предположения 
, то уравнения (2.4.1) эквивалентны следующим:
(2.4.6)
Доказательство.
Из j) и h) следует, что
. (2.4.7)
Отсюда, в частности, вытекает, что в силу k) 
.
Решение уравнений (2.4.6). Уравнения a)-e) и k) выражают тот факт, что коэффициенты 
и 
являются весами и узлами квадратурной формулы четвертого порядка при 
и . В силу (2.4.7) возможны следующие четыре случая:
1) 
. (2.4.8)
Тогда уравнения a)-e) образуют невырожденную линейную систему для определения 
. Эта система имеет решение:
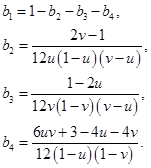
Остальные три случая с двойными узлами основаны на правиле Симпсона:
2) 
;
3) 
;
4) 
.
После того, как выбраны и , получаем 
из уравнения j), и тогда два уравнения f) и i) образуют линейную систему для определения 
и 
.
Определитель этой системы
,
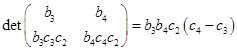согласно (2.4.7) не равен нулю. Наконец, из того, что 
находим 
, 
и 
.
Особенно популярными стали два варианта, которые выбрал Кутта в 1901 году. Это случай 3) при 
и случай 1) при 
. Оба метода обобщают классические квадратурные формулы, сохраняя их порядок. Первый из них более популярен, однако второй более точен.
Правило 3/8
|
|
|
|
|
Классический метод Рунге-Кутты
|
К-во Просмотров: 550
Бесплатно скачать Курсовая работа: Метод Рунге-Кутты четвертого порядка с автоматическим выбором шага интегрирования решения задачи Коши
|