Курсовая работа: Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

Справедлива следующая

Теорема 4.1 Пусть ≤p₀ <p₁ <∞, 1<q₀ ,q₁ ≤∞, M – произвольная сеть. Тогда

↪

где

Доказательство.

Учитывая, что ↪нам достаточно, доказать следующее вложение

↪

Пусть Рассмотрим произвольное представление a=a₀ +a₁ , где

тогда

(3)

Так как представление a=a₀ +a₁ произвольно, то из (3) следует

Где Рассматривая норму элемента в пространстве и применяя

лемму 4.4 , получаем:

Теорема доказана.

Теорема 4.2 Пусть 1≤p₀ <p₁ <∞, 1<q₀ ,q₁ ≤∞, Тогда имеет место равенство

Это равенство понимается в смысле эквивалентности норм с константами, не зависящими N.

Доказательство. По теореме 4.1 и того, что является обобщением пространств Лоренца нам достаточно доказать следующее вложение:

↩

.

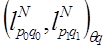Определим элементы и следующим образом

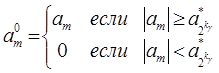
, тогда .

Заметим что