Курсовая работа: Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

Определим семейство конечномерных пространств

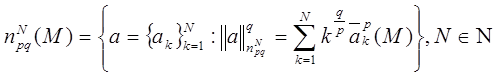
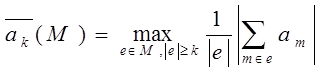
|e| - количество элементов множества e.

При q=∞ положим

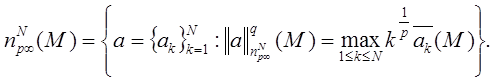
Данные пространства являются конечномерными аналогами сетевых пространств, введенных в [1].

Будем говорить что {A^N } ↪ {B^N } если существует константа c, такая что для любого , где c не зависит от .

Лемма 4.1 Пусть 1 ≤ q <q₁ ≤ ∞, 1 ≤ p ≤ ∞, . Тогда имеет место вложение

↪

то есть

где с не зависит от выбора N.

Доказательство. Пусть

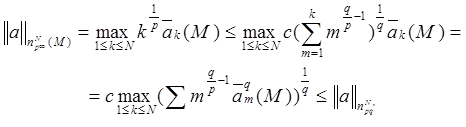(1)

то есть ↪

Теперь рассмотрим случай, когда 1 ≤ q <q₁ < ∞, и воспользуемся неравенством (1)

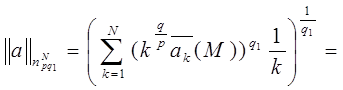
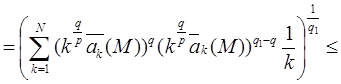
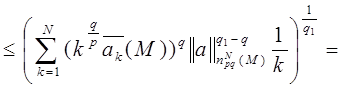
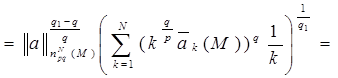
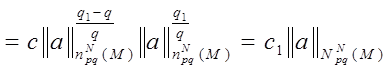
Лемма доказана.

Лемма 4.2 Пусть 1≤p<p₁ <∞, 1≤q,q₁ ≤∞. Тогда имеем место вложение

↪

Доказательство.

Согласно условию леммы, нам достаточно доказать вложения при p < p_{1 :}

↪

Получаем: