Курсовая работа: Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

где

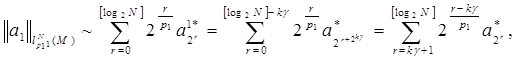(5)

где

Тогда

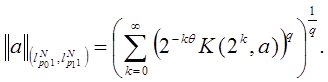
Из (4) и (5) имеем:

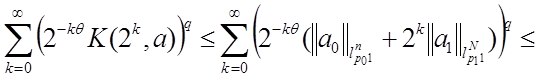
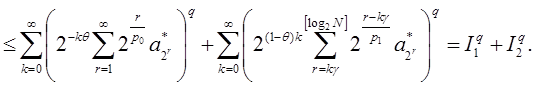
Оценим отдельно каждое из слагаемых последнего равенства, используя неравенство Гельдера:

~

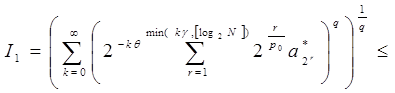
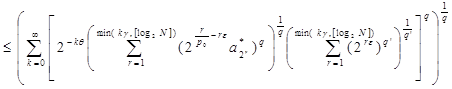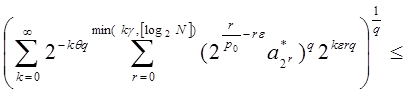
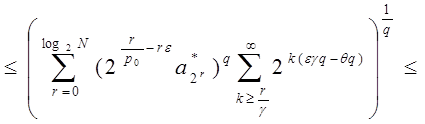
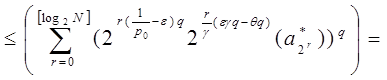
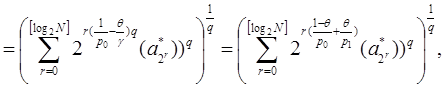
где .

Таким образом, получаем, что Аналогично рассмотрим второе слагаемое:

~

~

~

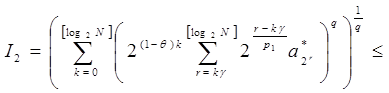
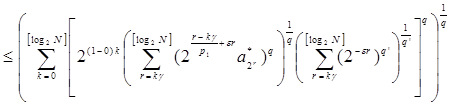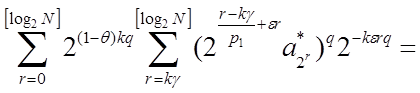
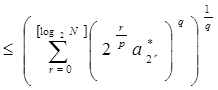Таким образом, получаем

где c не зависит от .

Теорема доказана.

Теорема 4.3 Пусть - матрица , тогда

~

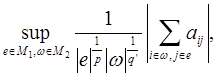
Причем соответствующие константы не зависят от