Курсовая работа: Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

Воспользуемся эквивалентными представлением нормы и неравенством о перестановках, получим

~

где - невозрастающая перестановка последовательности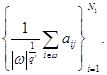

Применим неравенство Гельдера

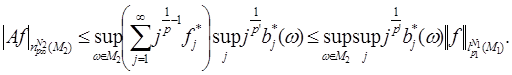
Учитывая лемму 3, имеем

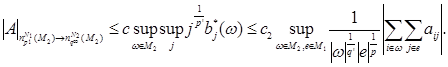
Обратно, пусть e произвольное множество из M₁ , , где

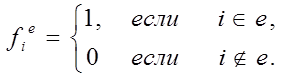
Тогда

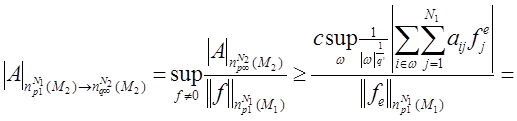
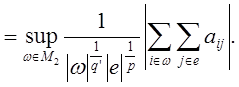
В силу произвольности выбора e из M₁ получаем требуемый результат.

Следствие. Пусть - матрица

p₀ <p₁ , q₀ <q₁ , тогда

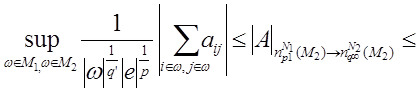
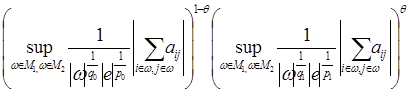
Доказательство. Из теоремы 3 следует, что

Воспользуемся интерполяционными теоремами 1,2, получаем

то есть

С другой стороны по лемме 1 и теореме 3 имеем

,

Следствие доказано.

Заключение