Так как в интервале равна постоянной температуре , а вне интервала температура равна нулю, то решение примет вид

Полученный результат можно преобразовать к интегралу вероятностей:

.

Действительно полагая , , получим

Таким образом, решение выразится формулой

Графиком функции является кривая:

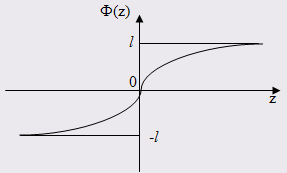
Найти решение уравнения , удовлетворяющее начальному условию и краевому условию .

Решение: Здесь мы имеем дифференциальное уравнение теплопроводности для полубесконечного стержня. Решение, удовлетворяющее указанным условиям, имеет вид

Или

Полагая , , преобразуем первый интеграл, пользуясь интегралом вероятностей, т.е.

Полагая , , получим

Таким образом, решение принимает вид

Заключение

В курсовой работе приведены некоторые примеры применения дифференциальных уравнений для моделирования таких реальных процессов, как колебания струны, распространение тепла в стержне.

Работа начинается с рассмотрения простейших задач, приводящих к дифференциальным уравнениям гиперболического типа (колебания струны, электрические колебания в проводах). Затем рассматривается один из методов решения уравнений данного типа. Во второй главе рассматриваются дифференциальные уравнения параболического типа (распространение тепловых волн) и одно из приложений к данной сфере – температурные волны.

Вследствие большого объема теории по применению дифференциальных уравнений для моделирования реальных процессов в данной курсовой работе не мог быть рассмотрен весь материал.

В заключение хотелось бы отметить особую роль дифференциальных уравнений при решении многих задач математики, физики и техники, так как часто не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях.

Литература

1. Н. С. Пискунов "Дифференциальное и интегральное исчисления", М., "Наука", 1972, том. 2.

2. И. М. Уваренков, М. З. Маллер "Курс математического анализа", М., "Просвещение", 1976.

3. А. Н. Тихонов, А. А. Самарский "Уравнения математической физики", М., "Наука", 1972.