Или

Глава 2. Уравнения параболического типа

2.1 Уравнение распространения тепла в стержне

Рассмотрим однородный стержень длины . Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.

Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = .

Рис. 2.1.

Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

(1)

где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.

Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 = х). Количество тепла, прошедшего через сечение с абсциссой х1 за время t, будет равно

(2)

то же самое с абсциссой х2:

(3)

Приток Q1 - Q2 в элемент стержня за время t будет равняться:

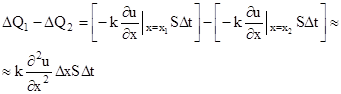(4)

Этот приток тепла за время t затратился на повышение температуры элемента стержня на величину u:

Или

(5)

где с – теплоемкость вещества стержня, – плотность вещества стержня (xS – масса элемента стержня).

Приравнивая выражения (4) и (5) одного и того же количества тепла , получим:

(6)

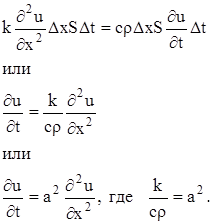
Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.

Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для , следующие:

u (x, 0) = φ(x), (7)

u (0, t) = ψ1(t), (8)