Курсовая работа: Некоторые уравнения математической физики в частных производных

(12)

где X (x) – функция только переменного x, T (t) – функция только переменного t.

Подставляя предполагаемую форму решения (12) в уравнение (1), получим:

или, после деления на XT,

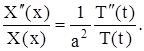(13)

Чтобы функция (12) была решением уравнения (1), равенство (13) должно удовлетворяться тождественно, т. е. 0 ‹ х ‹ , t › 0. Правая часть равенства (13) является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение

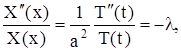(14)

где – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.

Из соотношения (14) получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t)

(15)

(16)

Граничные условия (11) дают:

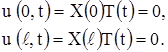
Отсюда следует, что функция X (x) должна удовлетворять дополнительным условиям:

X(0) = X() = 0, (17)

Так как иначе мы имели бы

в то время как задача состоит в нахождении нетривиального решения. Для функции T (t) в основной вспомогательной задаче никаких дополнительных условий нет.

Таким образом, в связи с нахождением функции X (x) мы приходим к простейшей задаче о собственных значениях: найти те значения параметра , при которых существуют нетривиальные решения задачи:

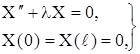(18)

а также найти эти решения. Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.

Рассмотрим отдельно случаи, когда параметр отрицателен, равен нулю или положителен.

1. При ‹ 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения (15) имеет вид

Граничные условия дают:

Х (0) = С1 + С2 = 0;

т. е.