Курсовая работа: Некоторые уравнения математической физики в частных производных

На концах этого элемента, по касательным к струне, действуют силы Т. Пусть касательные образуют с осью Ox углы . Тогда проекция на ось Ou сил, действующих на элемент , будет равна . Так как угол мал, то можно положить , и мы будем иметь:

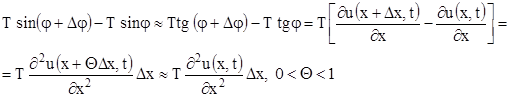
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).

Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть - линейная плотность струны. Тогда масса элемента струны будет . Ускорение элемента равно . Следовательно, по принципу Даламбера будем иметь:

.

Сокращая на и обозначая , получаем уравнение движения

.(1)

Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения движения струны одного уравнения (1) недостаточно. Искомая функция должна удовлетворять еще граничным условиям, указывающим, что делается на концах струны , и начальным условиям, описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.

Пусть, например, как мы предполагали, концы струны при неподвижны. Тогда при любом t должны выполнятся равенства:

(2’)

(2’’)

Эти равенства являются граничными условиями для нашей задачи.

В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f (x). Таким образом, должно быть

(3’)

Далее, в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией . Таким образом, должно быть

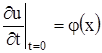(3’’)

Условия (3’) и (3’’) являются начальными условиями.

Замечание. В частности, может быть или . Если же и , то струна будет находится в покое, следовательно, .

1.3 Метод разделения переменных. Уравнение свободных колебаний струны

Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение уравнения

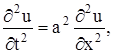
удовлетворяющее однородным граничным условиям

(9)

и начальным условиям

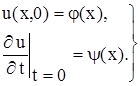(10)

Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение.

Поставим основную вспомогательную задачу: найти решение уравнения

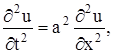
не равное тождественно нулю, удовлетворяющее однородным граничным условиям

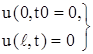(11)