Курсовая работа: Обработка информации и принятие решения в системах ближней локации

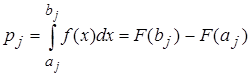, (20)

a_j и b_j – границы j -го интервала. Карл Пирсон показал, что, если все np_j ³ 5, то суммарная квадратическая относительная разность между теоретическим и практическим числом попаданий в интервал равна

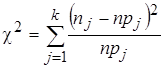(21)

имеет приближенно c² распределение Пирсона с k – m степенями свободы, где m – число параметров, оцениваемых по выборке, плюс 1. Так как параметров два, то m = 3. Выражение (21) представляет собой статистику Пирсона.

Теоретическое распределение можно считать подобранным верно, если выполняется условие

. (22)

Построим таблицу результатов, в которую занесем: номера интервалов (1-й столбец), границы интервалов a_j и b_j (2-й и 3-й столбцы), вероятность попадания в интервал p_j (4-й столбец), теоретическое число попаданий и практическое число попаданий np_j (6-й столбец). Границы интервалов и практическое число попаданий взяты из гистограммы, теоретическая вероятность попадания в j-й интервал подсчитывается по выражению (20).

Практическая часть.

clearTabl% очистили таблицу результатов

Tabl(:, 1)=[1:k]';% номера интервалов

Tabl(:, 2)=xm'-delta/2;% левые границы интервалов

Tabl(:, 3)=xm'+delta/2;% правые границы интервалов

Tabl(1,2)=-inf;% теоретическое начало 1-го интервала

Tabl(k, 3)=inf;% теоретический конец последнего интервала

Tabl(:, 4)=nj';% опытные числа попаданий

bor=[Tabl(:, 2); Tabl(end, 3)];% все границы интервалов

pro=cdf (tdistr{bdistr}, bor, param (bdistr, 1), param (bdistr, 2));

Tabl(:, 5)=pro (2:end) – pro (1:end-1);% вероятности попаданиz pj

Tabl(:, 6)=n*Tabl(:, 5);% теоретическоечислопопаданийnpj

disp('Сводная таблица результатов')

fprintf(' jajbj')

fprintf (' njpjnpj\n')

fprintf (' % 2.0f % 12.5f % 12.5f % 6.0f % 12.5f % 12.5f\n', Tabl')

Для сигнала гусеничной техники:

Сводная таблица результатов

j aj bj nj pj npj

1 – Inf -0.09544 2 0.00000 0.01837

2 -0.09544 -0.09464 2 0.00000 0.00408

3 -0.09464 -0.09385 0 0.00000 0.00495