Курсовая работа: Обработка информации и принятие решения в системах ближней локации

kstest(x, [xcdf(tdistr{idistr}, x,…

param(idistr, 1), param(idistr, 2))], 0. 1,0);

qq=[qqpkolm];% критические уровни значимости

end

[maxqq, bdistr]=max(qq);% выбрали лучшее распределение

fprintf(['Лучше всего подходит % s;\nкритический уровень '…

'значимости для него =%8.5f\n'], s{bdistr}, maxqq);

figure

cdfplot(x);% эмпирическая функция распределения

xpl=linspace(xl, xr, 500);% для графика F(x)

ypl=cdf (tdistr{bdistr}, xpl, param (bdistr, 1), param (bdistr, 2));

holdon% для рисования на этом же графике

plot(xpl, ypl, 'r');% дорисовали F(x)

hold off

set (get(gcf, 'CurrentAxes'),…

'FontName', 'Times New Roman Cyr', 'FontSize', 12)

title(['\bfПодобрано ' s{bdistr}])

xlabel ('\itx')% метка оси x

ylabel ('\itf\rm (\itx\rm)')% метка оси y

Результат:

Лучше всего подходит нормальное распределение;

критический уровень значимости для него = 0.31369

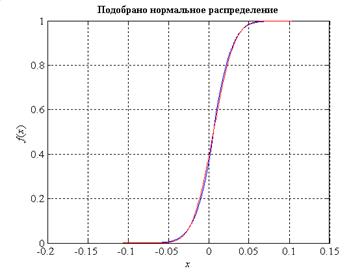
Рис. 11 – График эмпирической функции распределения для сигнала гусеничной техники

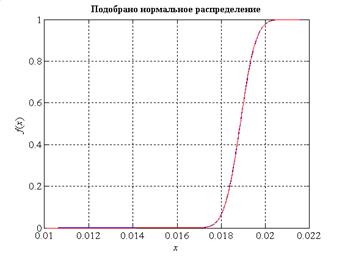
Рис. 12 – График эмпирической функции распределения для фонового сигнала

Найденный критический уровень значимости – это то значение q , при котором неравенство (19) обращается в равенство.

Вывод: По полученным результатам можно сделать вывод, что по данному критерию распределение подобранно верно.

1.6 Проверка гипотезы по критерию согласия Пирсона