Курсовая работа: Обработка информации и принятие решения в системах ближней локации
set (get(gcf, 'CurrentAxes'),…
'FontName', 'Times New Roman Cyr', 'FontSize', 12)
title('\bfПлотности распределения')
xlim([xlxr]), ylim([0 1.4*max(fv)])% границы рисунка по осям
xlabel('\itx')% метка оси x
ylabel('\itf\rm(\itx\rm)')% метка оси y
grid

Рис. 9 – График плотности распределения вероятности сигнала гусеничной техники и графики нормального, рэлеевского, показательного и равномерного законов плотностей распределения вероятности

Рис. 10 – График плотности распределения вероятности фонового сигнала и графики нормального, рэлеевского, показательного и равномерного законов плотностей распределения вероятности
Вывод: из рисунка 9 видно, что наиболее подходящим теоретическим распределением для первой эмпирической гистограммы является нормальное.
Реальный закон распределения амплитуд фонового сигнала также подчиняется нормальному закону.
1.5 Проверка гипотезы по критерию Колмогорова-Смирнова
Мы подобрали вид теоретического распределения и его параметры. Следующий этап – это проверка правильности подбора. Необходимо выяснить: насколько хорошо теоретическое распределение согласуется с данными. С этой целью используются критерии согласия Колмогорова-Смирнова или Пирсона., во втором – f (x ) и f * (x ).
Критерий согласия Колмогорова. В этом случае сравниваются теоретическая F (x ) и выборочная F * (x ) функции распределения. Сравниваемым параметром является максимальная по модулю разность между двумя функциями
 . (16)
. (16)
С точки зрения выборочного метода F * (x ) является случайной функцией, так как от выборки к выборке ее вид меняется, поэтому величина D является случайной. Согласно теореме Гливенко-Кантелли с ростом объема выборки эта величина сходится к нулю. Колмогоров А.Н. выяснил, как именно D сходится к нулю. Он рассмотрел случайную величину
![]() (17)
(17)
и нашел ее закон распределения. Как оказалось, при достаточно больших n он вообще не зависит от закона распределения генеральной совокупности X . Причем функция распределения случайной величины L имеет вид
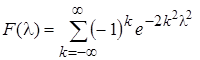 . (18)
. (18)
Если опытные данные x действительно взяты из генеральной совокупности с функцией распределения F (x ), то вычисленная по выражению (18) реализация l случайной величины L на уровне значимости q должна лежать в квантильных границах распределения Колмогорова (18). При этом, если l малое (выходит за «левый» квантиль), то нулевая гипотеза принимается: теоретическое распределение согласуется с опытными данными. В общем случае нулевая гипотеза принимается, если выполняется условие
l £ l1- q . (19)
Данный критерий называется еще критерием Колмогорова-Смирнова.
Таким образом, для применения критерия согласия Колмогорова-Смирнова, мы должны найти максимальную по модулю разность между выборочной и теоретической функциями распределения D по выражению (16), вычислить по ней l и проверить условие (19).
Практическая часть.
param=[[mxsx]; [lam 0]; [ab]; [sig 0]];% параметры распределений
qq=[];% критические уровни значимости
foridistr=1:ndistr, % критерий Колмогорова