Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений

1.2 Метод сведения линейной системы к одному уравнению более высокого порядка.

(Этот метод применим как для однородной, так и для неоднородной системы линейных дифференциальных уравнений.)

Один из методов интегрирования линейной системы заключается в сведении системы к одному уравнению n-ого порядка с одной неизвестной функцией. Продемонстрируем это на примере системы двух уравнений.

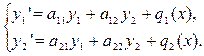(6)

Дифференцируя (по x) обе части первого уравнения системы (6), находим

откуда, заменяя производные y₁ ', y₂ ' их выражениями из самой системы, имеем

.

Группируя в правой части, получим уравнение вида

(7)

Где коэффициенты b₁ , b₂ и d₁ определенным образом выражаются через коэффициенты a_ij и q ₁ и их производные. Комбинируя уравнение (7) с первым уравнением системы (6), получим

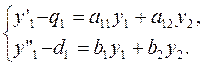(8)

Предположим, что в рассматриваемой области изменения x определитель

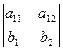
отличен от нуля. Тогда систему (8) можно решить относительно y₁ и y₂ , т.е. выразить y₁ и y₂ через y’₁ и y”₂ .

В результате приходим к уравнениям вида

(9)

. (10)

Первое из них представляет собой линейное дифференциальное уравнение второго порядка с одной неизвестной функцией y₁ (t). Заметим, что если в исходной системе (6) все коэффициенты a_ij постоянны, то уравнение (9) также является уравнением с постоянными коэффициентами. [ 3 стр 509-510]

1.3 Методы решения однородных линейных систем дифференциальных уравнений.

1) Сведение к одному уравнению n-ого порядка. (Этот метод мы разбирали выше)

2) Решение ЛОСДУ с постоянными коэффициентами с помощью матриц (видоизмененный метод Эйлера).

Пусть дана система n линейных дифференциальных уравнений с n неизвестными функциями, коэффициенты которой постоянные:

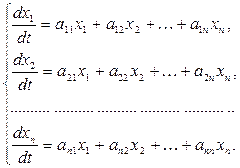(11)

Эту систему можно записать в виде одного матричного дифференциального уравнения

.

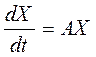Здесь

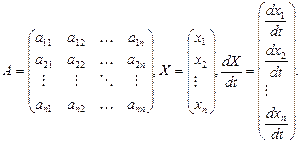
[2 стр 169]