Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений

Случай 1

Пример1.

Решение. Составляем характеристическое уравнение

Или . Находим корни:

Решение системы ищем в виде

и

.

Составим систему (3) для корня и определяем и :

Или

Откуда . Полагая , получаем . Таким образом, мы получили решение системы:

Составим далее систему (3) для корня и определяем и :

Откуда и =1, =1. Получаем второе решение системы:

Общее решение системы будет (см (6))

Пример2.

Решение. Составим характеристическое уравнение матрицы системы

или

Находим его корни:

Составим систему (3) для корня и определяем и :

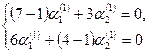или =>
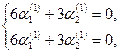