Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений

Где P₁ , P₂ – произвольные постоянные. Таким образом, общее решение системы имеет вид

Пример 2.

Решение. Составим характеристическое уравнение системы

Раскрывая определитель, получаем

Данное уравнение после несложных преобразовании принимает вид

Отсюда находим: (простой корень), ему соответствует собственный вектор

и (корень кратности 2), которому соответствуют два линейно независимых собственных вектора

Следовательно, общее решение системы имеет вид

2.3. решение неоднородных линейных систем дифференциальных уравнений.

2.3.1. Решение методом вариации постоянных.

Пример 1.

Решение. Решая характеристическое уравнение

Находим корни . Собственными векторами, отвечающими найденным собственным значениям, будут соответственно

,

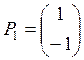Следовательно, общее решение соответствующей однородной системы имеет вид

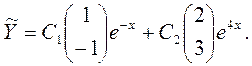
Решение неоднородного уравнения в соответствии с методом вариации постоянной будем искать в форме

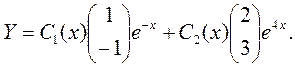
Для нахождения С₁ (x) и С₂ (x) подставив выражение для Y в исходную систему, получим