Курсовая работа: Однородные и неоднородные системы линейных дифференциальных уравнений

Отсюда находим:

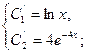
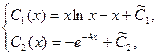
Где - произвольные постоянные. Таким образом, решение исходной системы будет

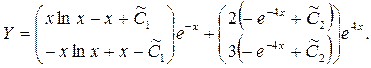
2.3.2. Решение методом неопределенных коэффициентов

Пример 1.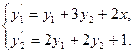

Решение. Решая характеристическое уравнение системы

Находим корни . Собственными векторами, отвечающими найденным собственным значениям, будут соответственно

,

Следовательно, общее решение соответствующей однородной системы имеет вид

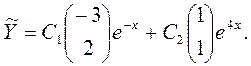
Теперь найдем частное решение. В рассматриваемом случае элементы столбца свободных членов представляют собой многочлены степени, не превышающей 1, и так как число γ=0 не совпадает с корнями характеристического уравнения, то частное решение неоднородной системы будем искать в виде

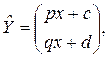
Где p, q, c и d – некоторые постоянные. Для их определения подставим выражение для в исходную систему. Получим

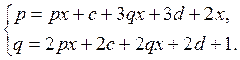
Отсюда

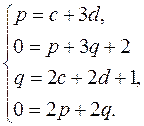
Решив эту систему, находим p=1, q= - 1, c= - 2 и d=1. Следовательно,

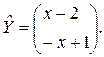
Так как общее решение неоднородной системы уравнения Y представляет собой сумму частного решения и общего решения соответствующей однородной системы, то окончательно получаем

Пример 2.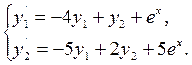

Решение. Решая характеристическое уравнение системы

Его корни будут . Им соответствуют собственные векторы

,